Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 84170 by jagoll last updated on 10/Mar/20

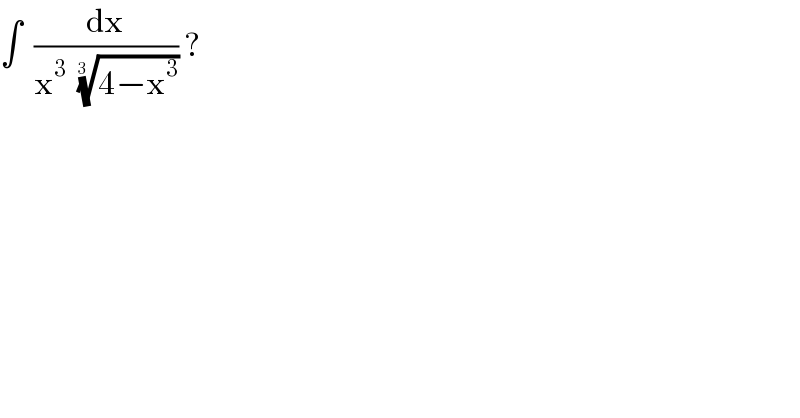
∫ (dx/(x^3 ((4−x^3 ))^(1/(3 )) )) ?

$$\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} \:\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{4}−\mathrm{x}^{\mathrm{3}} }}\:?\: \\ $$

Answered by john santu last updated on 10/Mar/20

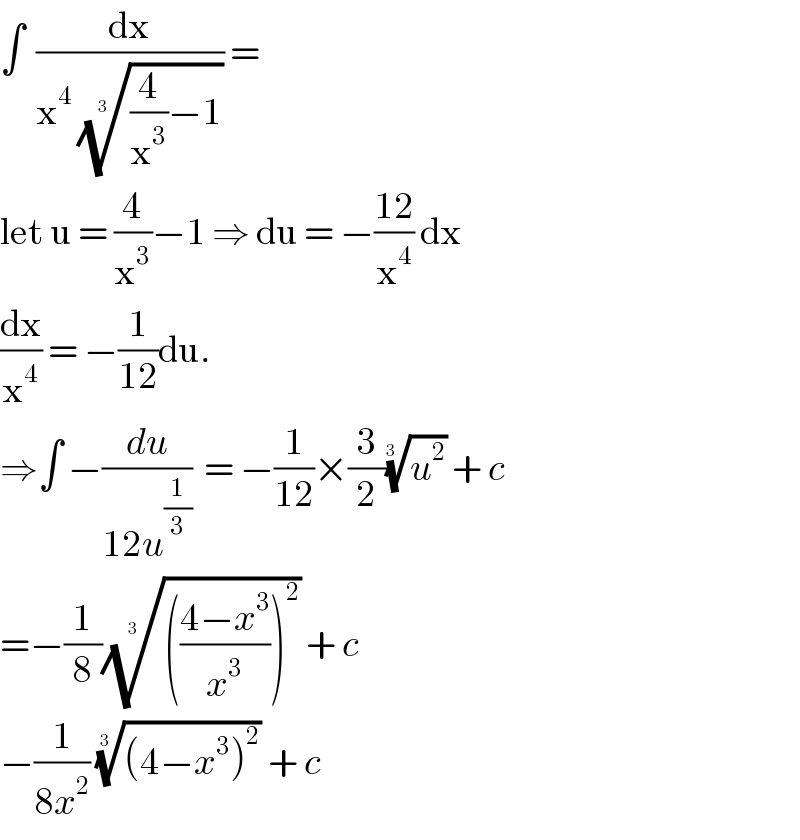
∫ (dx/(x^4 (((4/x^3 )−1))^(1/(3 )) )) = let u = (4/x^3 )−1 ⇒ du = −((12)/x^4 ) dx (dx/x^4 ) = −(1/(12))du. ⇒∫ −(du/(12u^(1/3) )) = −(1/(12))×(3/2)(u^2 )^(1/(3 )) + c =−(1/8)(((((4−x^3 )/x^3 ))^2 ))^(1/(3 )) + c −(1/(8x^2 )) (((4−x^3 )^2 ))^(1/(3 )) + c

$$\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} \:\sqrt[{\mathrm{3}\:\:}]{\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{3}} }−\mathrm{1}}}\:=\: \\ $$$$\mathrm{let}\:\mathrm{u}\:=\:\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{3}} }−\mathrm{1}\:\Rightarrow\:\mathrm{du}\:=\:−\frac{\mathrm{12}}{\mathrm{x}^{\mathrm{4}} }\:\mathrm{dx} \\ $$$$\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} }\:=\:−\frac{\mathrm{1}}{\mathrm{12}}\mathrm{du}. \\ $$$$\Rightarrow\int\:−\frac{{du}}{\mathrm{12}{u}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\:=\:−\frac{\mathrm{1}}{\mathrm{12}}×\frac{\mathrm{3}}{\mathrm{2}}\sqrt[{\mathrm{3}\:\:}]{{u}^{\mathrm{2}} }\:+\:{c} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{8}}\sqrt[{\mathrm{3}\:\:}]{\left(\frac{\mathrm{4}−{x}^{\mathrm{3}} }{{x}^{\mathrm{3}} }\right)^{\mathrm{2}} }\:+\:{c} \\ $$$$−\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{2}} }\:\sqrt[{\mathrm{3}\:\:}]{\left(\mathrm{4}−{x}^{\mathrm{3}} \right)^{\mathrm{2}} }\:+\:{c} \\ $$

Answered by MJS last updated on 10/Mar/20

∫(dx/(x^3 ((4−x^3 ))^(1/3) ))=−∫(dx/(x^3 ((x^3 −4))^(1/3) ))= [t=(((x^3 −4))^(1/3) /x) → dx=((x^2 (x^3 −4)^(2/3) )/4)] =−(1/4)∫tdt=−(1/8)t^2 =−(((x^3 −4)^(2/3) )/(8x^2 ))+C

$$\int\frac{{dx}}{{x}^{\mathrm{3}} \sqrt[{\mathrm{3}}]{\mathrm{4}−{x}^{\mathrm{3}} }}=−\int\frac{{dx}}{{x}^{\mathrm{3}} \sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} −\mathrm{4}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} −\mathrm{4}}}{{x}}\:\rightarrow\:{dx}=\frac{{x}^{\mathrm{2}} \left({x}^{\mathrm{3}} −\mathrm{4}\right)^{\mathrm{2}/\mathrm{3}} }{\mathrm{4}}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\int{tdt}=−\frac{\mathrm{1}}{\mathrm{8}}{t}^{\mathrm{2}} =−\frac{\left({x}^{\mathrm{3}} −\mathrm{4}\right)^{\mathrm{2}/\mathrm{3}} }{\mathrm{8}{x}^{\mathrm{2}} }+{C} \\ $$

Commented by john santu last updated on 10/Mar/20

oo thank you sir

$$\mathrm{oo}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by john santu last updated on 10/Mar/20

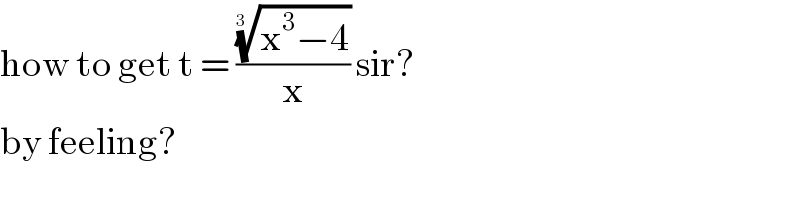
how to get t = (((x^3 −4))^(1/(3 )) /x) sir? by feeling?

$$\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\mathrm{t}\:=\:\frac{\sqrt[{\mathrm{3}\:\:}]{\mathrm{x}^{\mathrm{3}} −\mathrm{4}}}{\mathrm{x}}\:\mathrm{sir}? \\ $$$$\mathrm{by}\:\mathrm{feeling}? \\ $$

Commented by MJS last updated on 10/Mar/20

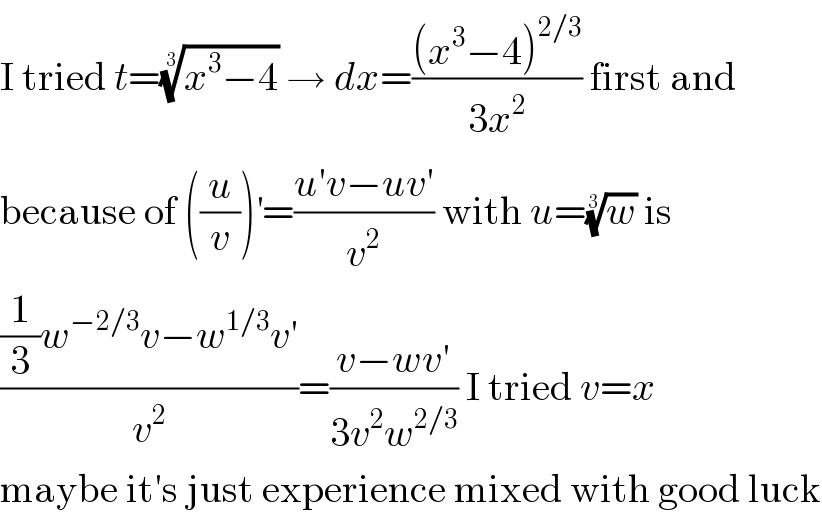
I tried t=((x^3 −4))^(1/3) → dx=(((x^3 −4)^(2/3) )/(3x^2 )) first and because of ((u/v))^′ =((u′v−uv′)/v^2 ) with u=(w)^(1/3) is (((1/3)w^(−2/3) v−w^(1/3) v′)/v^2 )=((v−wv′)/(3v^2 w^(2/3) )) I tried v=x maybe it′s just experience mixed with good luck

$$\mathrm{I}\:\mathrm{tried}\:{t}=\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} −\mathrm{4}}\:\rightarrow\:{dx}=\frac{\left({x}^{\mathrm{3}} −\mathrm{4}\right)^{\mathrm{2}/\mathrm{3}} }{\mathrm{3}{x}^{\mathrm{2}} }\:\mathrm{first}\:\mathrm{and} \\ $$$$\mathrm{because}\:\mathrm{of}\:\left(\frac{{u}}{{v}}\right)^{'} =\frac{{u}'{v}−{uv}'}{{v}^{\mathrm{2}} }\:\mathrm{with}\:{u}=\sqrt[{\mathrm{3}}]{{w}}\:\mathrm{is} \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{3}}{w}^{−\mathrm{2}/\mathrm{3}} {v}−{w}^{\mathrm{1}/\mathrm{3}} {v}'}{{v}^{\mathrm{2}} }=\frac{{v}−{wv}'}{\mathrm{3}{v}^{\mathrm{2}} {w}^{\mathrm{2}/\mathrm{3}} }\:\mathrm{I}\:\mathrm{tried}\:{v}={x} \\ $$$$\mathrm{maybe}\:\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{experience}\:\mathrm{mixed}\:\mathrm{with}\:\mathrm{good}\:\mathrm{luck} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com