Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 124607 by Mammadli last updated on 04/Dec/20

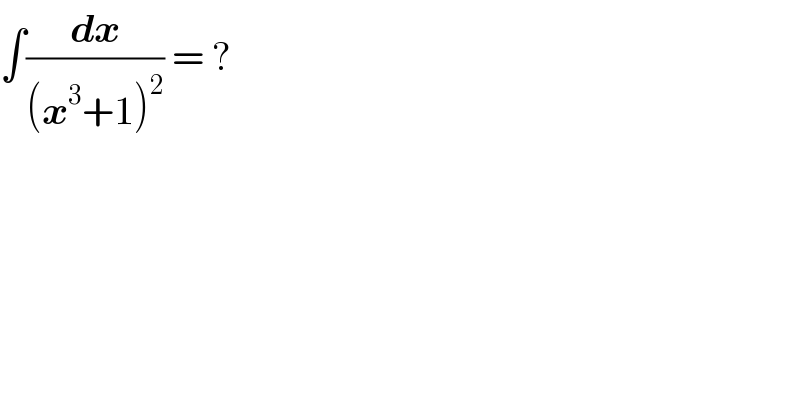
∫(dx/((x^3 +1)^2 )) = ?

$$\int\frac{\boldsymbol{{dx}}}{\left(\boldsymbol{{x}}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }\:=\:? \\ $$

Answered by MJS_new last updated on 04/Dec/20

(1) Ostrogradski′s Method: ∫(dx/((x^3 +1)^2 ))=((ax^2 +bx+c)/(x^3 +1))+∫((dx^2 +ex+f)/(x^3 +1))dx (1/((x^3 +1)^2 ))=(d/dx)[((ax^2 +bx+c)/(x^3 +1))]+((dx^2 +ex+f)/(x^3 +1)) ⇒ ∫(dx/((x^3 +1)))=(x/(3(x^3 +1)))+(2/3)∫(dx/(x^3 +1)) )(2) Decomposition (2/3)∫(dx/(x^3 +1))=(2/9)∫(dx/(x+1))−(2/9)∫((x−2)/(x^2 −x+1))dx= =(2/9)∫(dx/(x+1))−(1/9)∫((2x−1)/(x^2 −x+1))dx+(1/3)∫(dx/(x^2 −x+1))= =(2/9)ln (x+1) −(1/9)ln (x^2 −x+1) +((2(√3))/9)arctan (((√3)(2x−1))/3) = =(1/9)ln (((x+1)^2 )/(x^2 −x+1)) +((2(√3))/9)arctan (((√3)(2x−1))/3) ⇒ answer is ∫(dx/((x^3 +1)^2 ))= =(x/(3(x^3 +1)))+(1/9)ln (((x+1)^2 )/(x^2 −x+1)) +((2(√3))/9)arctan (((√3)(2x−1))/3) +C

$$\left(\mathrm{1}\right)\:\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}: \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }=\frac{{ax}^{\mathrm{2}} +{bx}+{c}}{{x}^{\mathrm{3}} +\mathrm{1}}+\int\frac{{dx}^{\mathrm{2}} +{ex}+{f}}{{x}^{\mathrm{3}} +\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }=\frac{{d}}{{dx}}\left[\frac{{ax}^{\mathrm{2}} +{bx}+{c}}{{x}^{\mathrm{3}} +\mathrm{1}}\right]+\frac{{dx}^{\mathrm{2}} +{ex}+{f}}{{x}^{\mathrm{3}} +\mathrm{1}} \\ $$$$\Rightarrow \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{3}} +\mathrm{1}\right)}=\frac{{x}}{\mathrm{3}\left({x}^{\mathrm{3}} +\mathrm{1}\right)}+\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dx}}{{x}^{\mathrm{3}} +\mathrm{1}} \\ $$$$\left.\right)\left(\mathrm{2}\right)\:\mathrm{Decomposition} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dx}}{{x}^{\mathrm{3}} +\mathrm{1}}=\frac{\mathrm{2}}{\mathrm{9}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{9}}\int\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{9}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{9}}\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{9}}\mathrm{ln}\:\left({x}+\mathrm{1}\right)\:−\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\:+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{3}}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{3}} \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is} \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=\frac{{x}}{\mathrm{3}\left({x}^{\mathrm{3}} +\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{3}}\:+{C} \\ $$

Commented by Dwaipayan Shikari last updated on 04/Dec/20

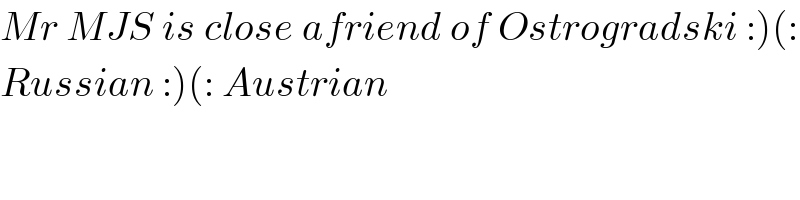
Mr MJS is close afriend of Ostrogradski :)(: Russian :)(: Austrian

$$\left.{Mr}\:{MJS}\:{is}\:{close}\:{afriend}\:{of}\:{Ostrogradski}\::\right)\left(:\right. \\ $$$$\left.{Russian}\::\right)\left(:\:{Austrian}\right. \\ $$

Commented by MJS_new last updated on 04/Dec/20

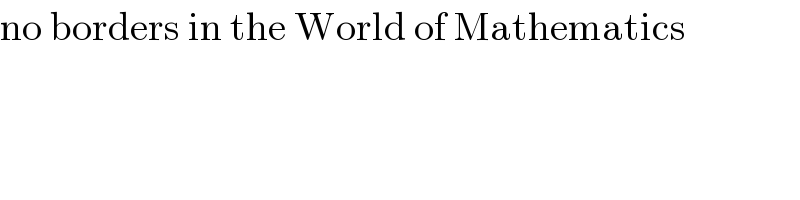
no borders in the World of Mathematics

$$\mathrm{no}\:\mathrm{borders}\:\mathrm{in}\:\mathrm{the}\:\mathrm{World}\:\mathrm{of}\:\mathrm{Mathematics} \\ $$

Commented by bemath last updated on 05/Dec/20

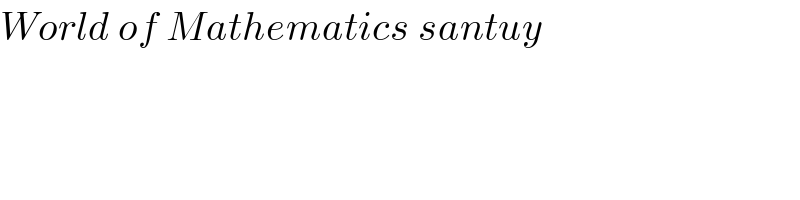
World of Mathematics santuy

$${World}\:{of}\:{Mathematics}\:{santuy} \\ $$

Answered by mathmax by abdo last updated on 05/Dec/20

parametric method let f(a) =∫ (dx/(x^3 +a^3 )) ⇒ f^′ (a) =−∫ ((3a^2 )/((x^3 +a^3 )^2 ))dx ⇒f^′ (1) =−3∫(dx/((x^3 +1)^2 )) ⇒ ∫ (dx/((x^3 +1)^2 ))=−(1/3)f^′ (1) let explicite f(a) let decompose F(x)=(1/(x^3 +a^3 ))=(1/((x+a)(x^2 −ax +a^2 ))) ⇒ F(x)=(α/(x+a))+((βx+λ)/(x^2 −ax +a^2 )) α=(1/(3a^2 )) ,lim_(x→+∞) xF(x)=0 =α+β ⇒β=−(1/(3a^2 )) ⇒ F(x)=(1/(3a^2 (x+a)))+((−(1/(3a^2 ))x+λ)/(x^2 −ax +a^2 )) F(0)=(1/a^3 )=(α/a)+(λ/a^2 ) ⇒1 =a^2 α+aλ ⇒aλ=1−a^2 (1/(3a^2 ))=(2/3) ⇒ λ=(2/(3a)) ⇒F(x)=(1/(3a^2 (x+a)))+((−(1/(3a^2 ))x+(2/(3a)))/(x^2 −ax +a^2 )) ⇒ ∫ F(x)dx=(1/(3a^2 ))∫ (dx/(x+a))−(1/(3a^2 ))∫((x+2a)/(x^2 −ax+a^2 ))dx =(1/(3a^2 ))ln∣x+a∣−(1/(6a^2 ))∫ ((2x−a+5a)/(x^2 −ax +a^2 ))dx =(1/(3a^2 ))ln∣x+a∣−(1/(6a^2 ))ln(x^2 −ax+a^2 )−(5/(6a))∫ (dx/(x^2 −ax+a^2 )) rest calculus of ∫ (dx/(x^2 −ax+a^2 ))...be continued....

$$\mathrm{parametric}\:\mathrm{method}\:\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} \:+\mathrm{a}^{\mathrm{3}} }\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\int\:\:\frac{\mathrm{3a}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{3}} \:+\mathrm{a}^{\mathrm{3}} \right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{1}\right)\:=−\mathrm{3}\int\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{3}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{f}^{'} \left(\mathrm{1}\right)\:\:\mathrm{let}\:\mathrm{explicite}\:\mathrm{f}\left(\mathrm{a}\right) \\ $$$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} \:+\mathrm{a}^{\mathrm{3}} }=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{a}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{ax}\:+\mathrm{a}^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\frac{\alpha}{\mathrm{x}+\mathrm{a}}+\frac{\beta\mathrm{x}+\lambda}{\mathrm{x}^{\mathrm{2}} −\mathrm{ax}\:+\mathrm{a}^{\mathrm{2}} } \\ $$$$\alpha=\frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} }\:\:,\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{xF}\left(\mathrm{x}\right)=\mathrm{0}\:=\alpha+\beta\:\Rightarrow\beta=−\frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} \left(\mathrm{x}+\mathrm{a}\right)}+\frac{−\frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} }\mathrm{x}+\lambda}{\mathrm{x}^{\mathrm{2}} \:−\mathrm{ax}\:+\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{F}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{3}} }=\frac{\alpha}{\mathrm{a}}+\frac{\lambda}{\mathrm{a}^{\mathrm{2}} }\:\Rightarrow\mathrm{1}\:=\mathrm{a}^{\mathrm{2}} \alpha+\mathrm{a}\lambda\:\Rightarrow\mathrm{a}\lambda=\mathrm{1}−\mathrm{a}^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow \\ $$$$\lambda=\frac{\mathrm{2}}{\mathrm{3a}}\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} \left(\mathrm{x}+\mathrm{a}\right)}+\frac{−\frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} }\mathrm{x}+\frac{\mathrm{2}}{\mathrm{3a}}}{\mathrm{x}^{\mathrm{2}} −\mathrm{ax}\:+\mathrm{a}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:\mathrm{F}\left(\mathrm{x}\right)\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} }\int\:\:\frac{\mathrm{dx}}{\mathrm{x}+\mathrm{a}}−\frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} }\int\frac{\mathrm{x}+\mathrm{2a}}{\mathrm{x}^{\mathrm{2}} −\mathrm{ax}+\mathrm{a}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} }\mathrm{ln}\mid\mathrm{x}+\mathrm{a}\mid−\frac{\mathrm{1}}{\mathrm{6a}^{\mathrm{2}} }\int\:\frac{\mathrm{2x}−\mathrm{a}+\mathrm{5a}}{\mathrm{x}^{\mathrm{2}} −\mathrm{ax}\:+\mathrm{a}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3a}^{\mathrm{2}} }\mathrm{ln}\mid\mathrm{x}+\mathrm{a}\mid−\frac{\mathrm{1}}{\mathrm{6a}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{ax}+\mathrm{a}^{\mathrm{2}} \right)−\frac{\mathrm{5}}{\mathrm{6a}}\int\:\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{ax}+\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{rest}\:\mathrm{calculus}\:\mathrm{of}\:\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{ax}+\mathrm{a}^{\mathrm{2}} }...\mathrm{be}\:\mathrm{continued}.... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com