Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 65988 by mmkkmm000m last updated on 07/Aug/19

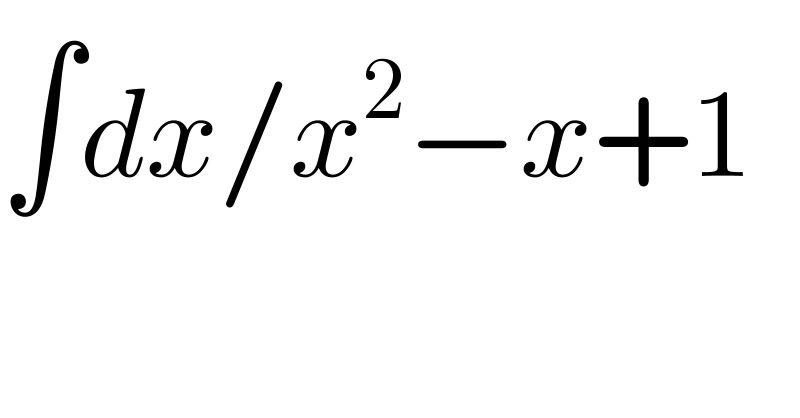
∫dx/x^2 −x+1

$$\int{dx}/{x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$

Commented by mathmax by abdo last updated on 07/Aug/19

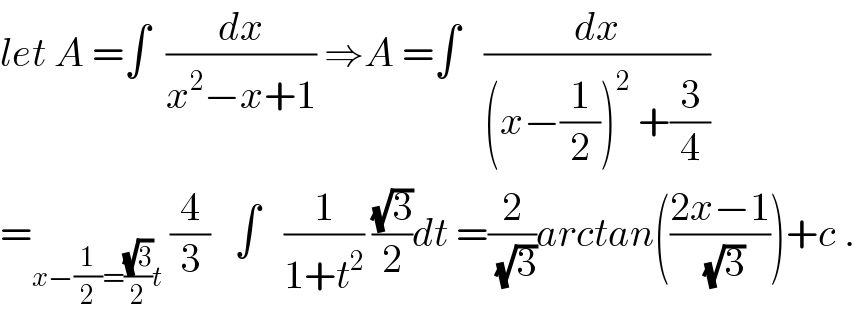
let A =∫ (dx/(x^2 −x+1)) ⇒A =∫ (dx/((x−(1/2))^2 +(3/4))) =_(x−(1/2)=((√3)/2)t) (4/3) ∫ (1/(1+t^2 )) ((√3)/2)dt =(2/(√3))arctan(((2x−1)/(√3)))+c .

$${let}\:{A}\:=\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:\Rightarrow{A}\:=\int\:\:\:\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=_{{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}} \:\frac{\mathrm{4}}{\mathrm{3}}\:\:\:\int\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt}\:=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)+{c}\:. \\ $$

Answered by meme last updated on 07/Aug/19

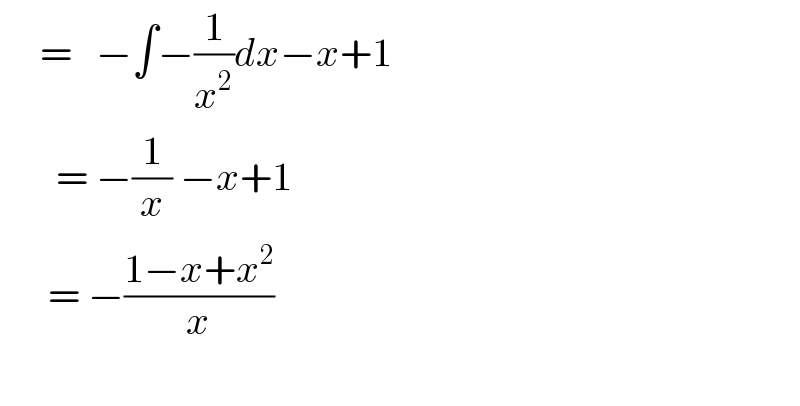
= −∫−(1/x^2 )dx−x+1 = −(1/x) −x+1 = −((1−x+x^2 )/x)

$$\:\:\:\:\:=\:\:\:−\int−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx}−{x}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:=\:−\frac{\mathrm{1}}{{x}}\:−{x}+\mathrm{1} \\ $$$$\:\:\:\:\:\:=\:−\frac{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{{x}} \\ $$$$\:\:\:\:\:\: \\ $$

Answered by meme last updated on 07/Aug/19

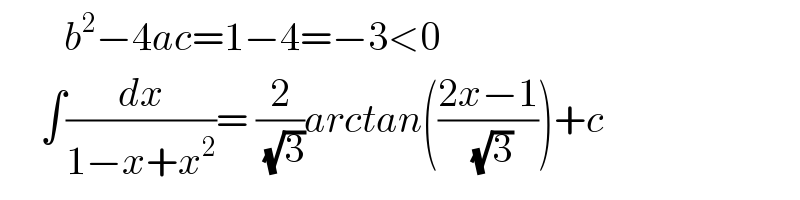
b^2 −4ac=1−4=−3<0 ∫(dx/(1−x+x^2 ))= (2/(√3))arctan(((2x−1)/(√3)))+c

$$\:\:\:\:\:\:\:\:{b}^{\mathrm{2}} −\mathrm{4}{ac}=\mathrm{1}−\mathrm{4}=−\mathrm{3}<\mathrm{0} \\ $$$$\:\:\:\:\:\int\frac{{dx}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }=\:\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)+{c} \\ $$

Answered by AnjanDey last updated on 07/Aug/19

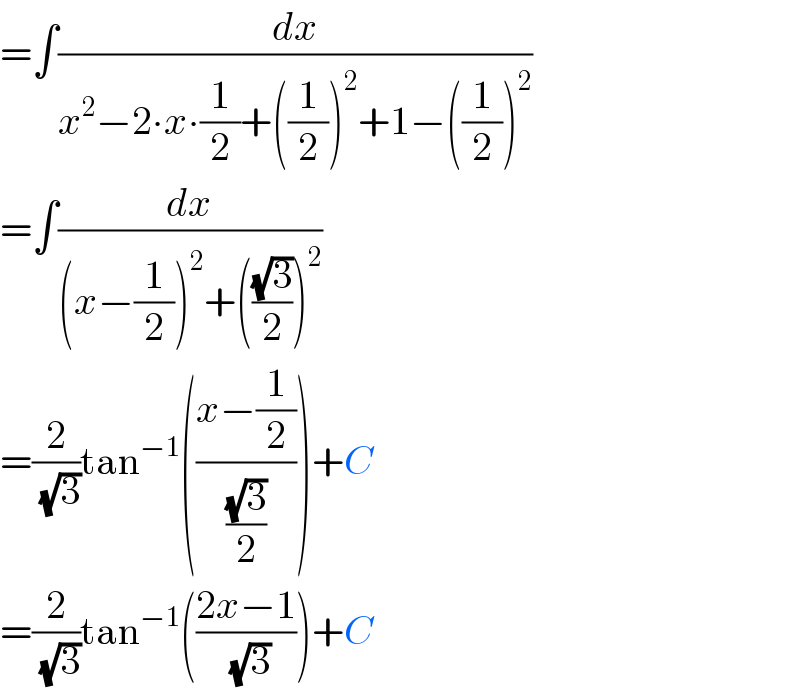
=∫(dx/(x^2 −2∙x∙(1/2)+((1/2))^2 +1−((1/2))^2 )) =∫(dx/((x−(1/2))^2 +(((√3)/2))^2 )) =(2/(√3))tan^(−1) (((x−(1/2))/((√3)/2)))+C =(2/(√3))tan^(−1) (((2x−1)/(√3)))+C

$$=\int\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}\centerdot{x}\centerdot\frac{\mathrm{1}}{\mathrm{2}}+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\int\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right)+{C} \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com