Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 129635 by pticantor last updated on 17/Jan/21

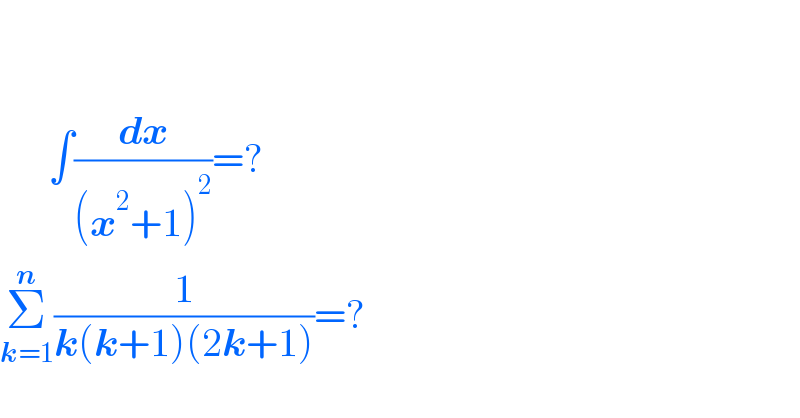
∫(dx/((x^2 +1)^2 ))=? Σ_(k=1) ^n (1/(k(k+1)(2k+1)))=?

$$\:\:\:\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\int\frac{\boldsymbol{{dx}}}{\left(\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }=? \\ $$$$\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\frac{\mathrm{1}}{\boldsymbol{{k}}\left(\boldsymbol{{k}}+\mathrm{1}\right)\left(\mathrm{2}\boldsymbol{{k}}+\mathrm{1}\right)}=? \\ $$

Commented by liberty last updated on 17/Jan/21

(1/(k(k+1)(2k+1))) = (a/k)+(b/(k+1))+(c/(2k+1)) a= [ (1/((k+1)(2k+1))) ]_(k=0) = 1 b = [ (1/(k(2k+1))) ]_(k=−1) = 1 c = [ (1/(k(k+1))) ]_(k=−(1/2)) = −4

$$\:\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{2k}+\mathrm{1}\right)}\:=\:\frac{\mathrm{a}}{\mathrm{k}}+\frac{\mathrm{b}}{\mathrm{k}+\mathrm{1}}+\frac{\mathrm{c}}{\mathrm{2k}+\mathrm{1}} \\ $$$$\:\mathrm{a}=\:\left[\:\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{2k}+\mathrm{1}\right)}\:\right]_{\mathrm{k}=\mathrm{0}} =\:\mathrm{1} \\ $$$$\:\mathrm{b}\:=\:\left[\:\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{2k}+\mathrm{1}\right)}\:\right]_{\mathrm{k}=−\mathrm{1}} =\:\mathrm{1} \\ $$$$\:\mathrm{c}\:=\:\left[\:\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)}\:\right]_{\mathrm{k}=−\frac{\mathrm{1}}{\mathrm{2}}} =\:−\mathrm{4} \\ $$$$ \\ $$

Answered by Dwaipayan Shikari last updated on 17/Jan/21

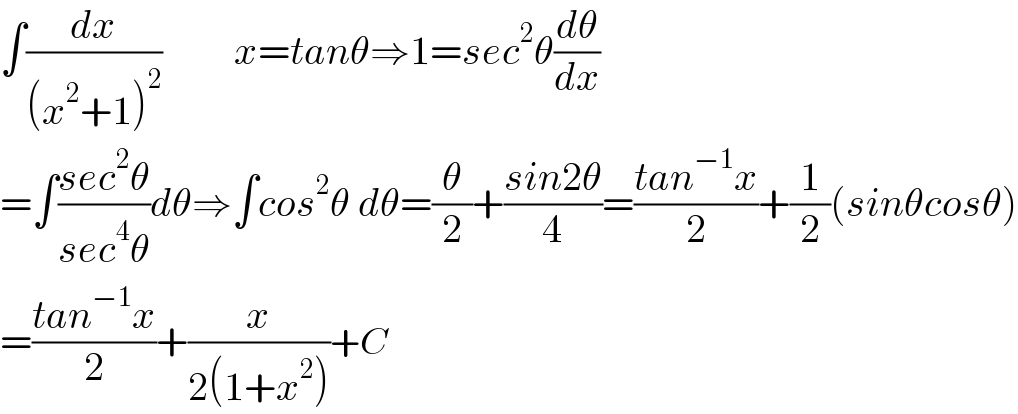
∫(dx/((x^2 +1)^2 )) x=tanθ⇒1=sec^2 θ(dθ/dx) =∫((sec^2 θ)/(sec^4 θ))dθ⇒∫cos^2 θ dθ=(θ/2)+((sin2θ)/4)=((tan^(−1) x)/2)+(1/2)(sinθcosθ) =((tan^(−1) x)/2)+(x/(2(1+x^2 )))+C

$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:{x}={tan}\theta\Rightarrow\mathrm{1}={sec}^{\mathrm{2}} \theta\frac{{d}\theta}{{dx}} \\ $$$$=\int\frac{{sec}^{\mathrm{2}} \theta}{{sec}^{\mathrm{4}} \theta}{d}\theta\Rightarrow\int{cos}^{\mathrm{2}} \theta\:{d}\theta=\frac{\theta}{\mathrm{2}}+\frac{{sin}\mathrm{2}\theta}{\mathrm{4}}=\frac{{tan}^{−\mathrm{1}} {x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\left({sin}\theta{cos}\theta\right) \\ $$$$=\frac{{tan}^{−\mathrm{1}} {x}}{\mathrm{2}}+\frac{{x}}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}+{C} \\ $$

Answered by mathmax by abdo last updated on 17/Jan/21

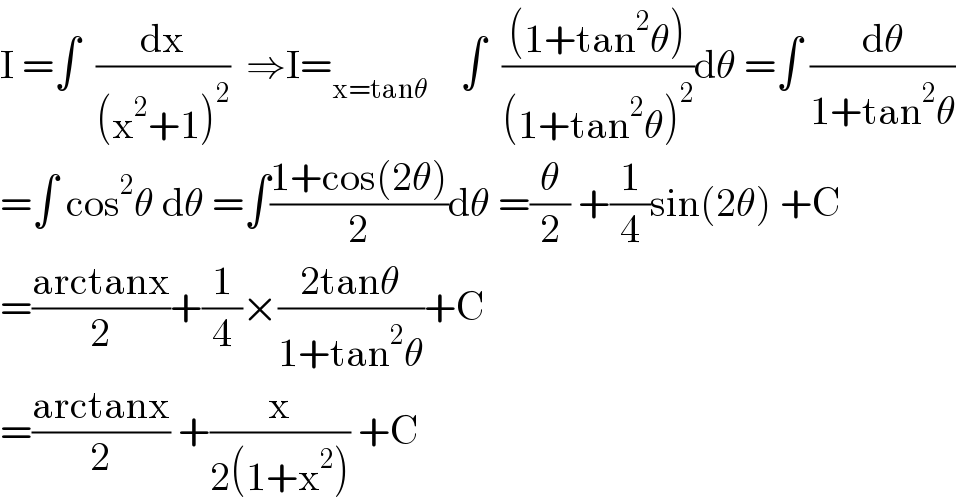
I =∫ (dx/((x^2 +1)^2 )) ⇒I=_(x=tanθ) ∫ (((1+tan^2 θ))/((1+tan^2 θ)^2 ))dθ =∫ (dθ/(1+tan^2 θ)) =∫ cos^2 θ dθ =∫((1+cos(2θ))/2)dθ =(θ/2) +(1/4)sin(2θ) +C =((arctanx)/2)+(1/4)×((2tanθ)/(1+tan^2 θ))+C =((arctanx)/2) +(x/(2(1+x^2 ))) +C

$$\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\:\Rightarrow\mathrm{I}=_{\mathrm{x}=\mathrm{tan}\theta} \:\:\:\:\int\:\:\frac{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\mathrm{d}\theta\:=\int\:\frac{\mathrm{d}\theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta} \\ $$$$=\int\:\mathrm{cos}^{\mathrm{2}} \theta\:\mathrm{d}\theta\:=\int\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\mathrm{d}\theta\:=\frac{\theta}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{2}\theta\right)\:+\mathrm{C} \\ $$$$=\frac{\mathrm{arctanx}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{2tan}\theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}+\mathrm{C} \\ $$$$=\frac{\mathrm{arctanx}}{\mathrm{2}}\:+\frac{\mathrm{x}}{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\:+\mathrm{C} \\ $$

Answered by mathmax by abdo last updated on 17/Jan/21

let decompose F(x)=(1/(x(x+1)(2x+1))) ⇒F(x)=(a/x)+(b/(x+1))+(c/(2x+1)) a=1 ,b=1 , c=(1/((−(1/2))((1/2))))=−4 ⇒F(x)=(1/x)+(1/(x+1))−(4/(2x+1)) ⇒ S_n =Σ_(k=1) ^n (1/(k(k+1)(2k+1))) =Σ_(k=1) ^n (1/k)+Σ_(k=1) ^n (1/(k+1))−4 Σ_(k=1) ^n (1/(2k+1)) Σ_(k=1) ^n =H_n ,Σ_(k=1) ^n (1/(k+1))=Σ_(k=2) ^(n+1) (1/k)=H_(n+1) −1 Σ_(k=1) ^n (1/(2k+1))=(1/3)+(1/5)+....+(1/(2n+1)) =1+(1/2)+(1/3)+(1/4)+(1/5)+....+(1/(2n))+(1/(2n+1)) −1−(1/2)(1+(1/2)+...+(1/n)) =H_(2n+1) −(1/2)H_n −1 ⇒ S_n =H_n +H_(n+1) −1 −4(H_(2n+1) −(1/2)H_n −1) =H_n +H_(n+1) −1−4H_(2n+1) +2H_n +4 =2H_n +(1/(n+1))−4H_(2n+1) +3+2H_n =4 H_n −4H_(2n+1) +3

$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{2x}+\mathrm{1}\right)}\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{a}}{\mathrm{x}}+\frac{\mathrm{b}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{c}}{\mathrm{2x}+\mathrm{1}} \\ $$$$\mathrm{a}=\mathrm{1}\:\:,\mathrm{b}=\mathrm{1}\:\:,\:\mathrm{c}=\frac{\mathrm{1}}{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}=−\mathrm{4}\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{4}}{\mathrm{2x}+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{2k}+\mathrm{1}\right)}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}+\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}−\mathrm{4}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{2k}+\mathrm{1}} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:=\mathrm{H}_{\mathrm{n}} \:\:,\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}=\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{k}}=\mathrm{H}_{\mathrm{n}+\mathrm{1}} −\mathrm{1} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{2k}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+....+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}+....+\frac{\mathrm{1}}{\mathrm{2n}}+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\:−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+...+\frac{\mathrm{1}}{\mathrm{n}}\right) \\ $$$$=\mathrm{H}_{\mathrm{2n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{H}_{\mathrm{n}} −\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{S}_{\mathrm{n}} =\mathrm{H}_{\mathrm{n}} \:+\mathrm{H}_{\mathrm{n}+\mathrm{1}} −\mathrm{1}\:−\mathrm{4}\left(\mathrm{H}_{\mathrm{2n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{H}_{\mathrm{n}} −\mathrm{1}\right) \\ $$$$=\mathrm{H}_{\mathrm{n}} \:+\mathrm{H}_{\mathrm{n}+\mathrm{1}} −\mathrm{1}−\mathrm{4H}_{\mathrm{2n}+\mathrm{1}} +\mathrm{2H}_{\mathrm{n}} \:+\mathrm{4} \\ $$$$=\mathrm{2H}_{\mathrm{n}} \:+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\mathrm{4H}_{\mathrm{2n}+\mathrm{1}} +\mathrm{3}+\mathrm{2H}_{\mathrm{n}} \\ $$$$=\mathrm{4}\:\mathrm{H}_{\mathrm{n}} −\mathrm{4H}_{\mathrm{2n}+\mathrm{1}} \:+\mathrm{3} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com