Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 126000 by bramlexs22 last updated on 16/Dec/20

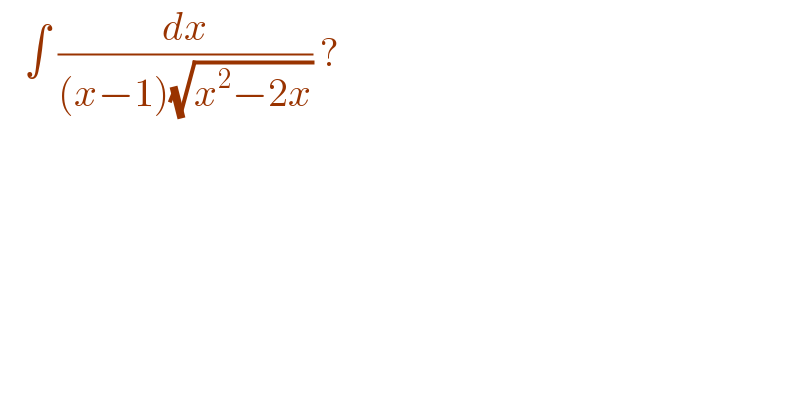
∫ (dx/((x−1)(√(x^2 −2x)))) ?

$$\:\:\:\int\:\frac{{dx}}{\left({x}−\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}}}\:? \\ $$

Answered by Dwaipayan Shikari last updated on 16/Dec/20

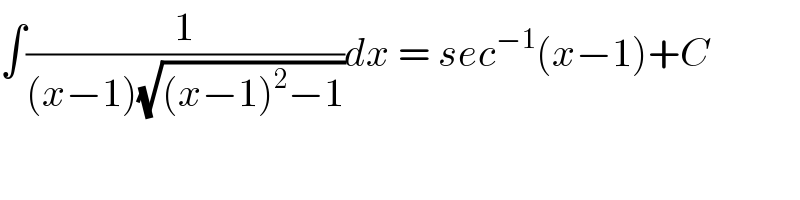
∫(1/((x−1)(√((x−1)^2 −1))))dx = sec^(−1) (x−1)+C

$$\int\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)\sqrt{\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}}{dx}\:=\:{sec}^{−\mathrm{1}} \left({x}−\mathrm{1}\right)+{C} \\ $$

Commented by bramlexs22 last updated on 16/Dec/20

yes..thanks

$${yes}..{thanks} \\ $$

Answered by benjo_mathlover last updated on 16/Dec/20

μ = ∫ (dx/((x−1)(√((x−1)^2 −1)))) μ = ∫ ((d(x−1))/((x−1)(√((x−1)^2 −1)))) μ = ∫ (dX/(X (√(X^2 −1)))) [ X = sec w ] μ = ∫ ((sec w tan w)/(sec w tan w)) dw = w + c μ = sec^(−1) (X)+c = sec^(−1) (x−1)+c

$$\:\mu\:=\:\int\:\frac{{dx}}{\left({x}−\mathrm{1}\right)\sqrt{\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\:\mu\:=\:\int\:\frac{{d}\left({x}−\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)\sqrt{\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\:\mu\:=\:\int\:\frac{{dX}}{{X}\:\sqrt{{X}^{\mathrm{2}} −\mathrm{1}}}\:\:\left[\:{X}\:=\:\mathrm{sec}\:{w}\:\right]\: \\ $$$$\:\mu\:=\:\int\:\frac{\mathrm{sec}\:{w}\:\mathrm{tan}\:{w}}{\mathrm{sec}\:{w}\:\mathrm{tan}\:{w}}\:{dw}\:=\:{w}\:+\:{c}\: \\ $$$$\:\mu\:=\:\mathrm{sec}^{−\mathrm{1}} \left({X}\right)+{c}\:=\:\mathrm{sec}^{−\mathrm{1}} \left({x}−\mathrm{1}\right)+{c}\: \\ $$

Answered by mathmax by abdo last updated on 16/Dec/20

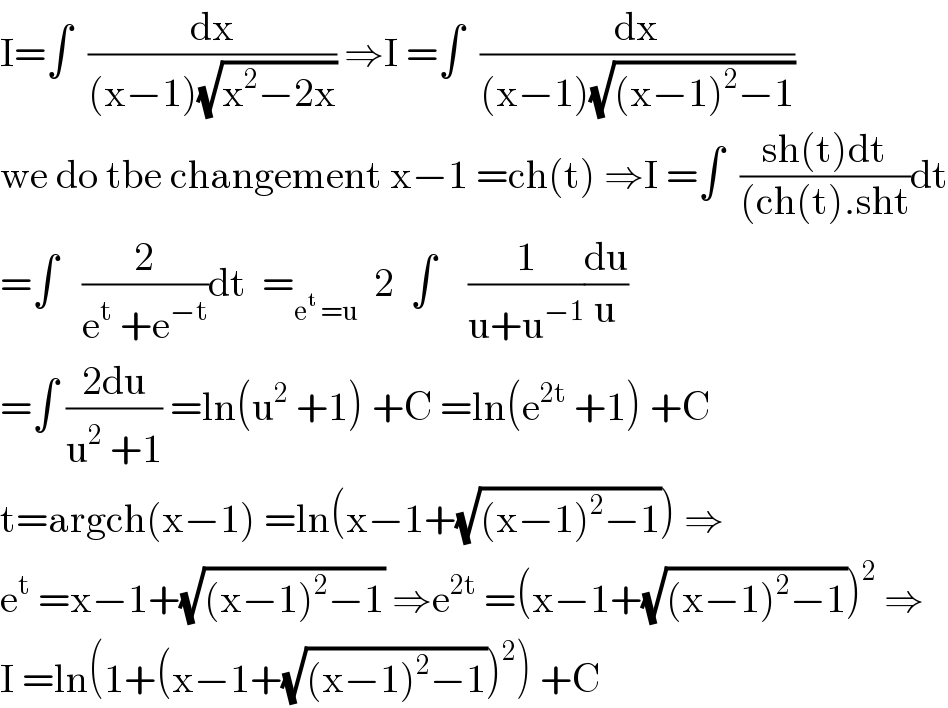
I=∫ (dx/((x−1)(√(x^2 −2x)))) ⇒I =∫ (dx/((x−1)(√((x−1)^2 −1)))) we do tbe changement x−1 =ch(t) ⇒I =∫ ((sh(t)dt)/((ch(t).sht))dt =∫ (2/(e^t +e^(−t) ))dt =_(e^t =u) 2 ∫ (1/(u+u^(−1) ))(du/u) =∫ ((2du)/(u^2 +1)) =ln(u^2 +1) +C =ln(e^(2t) +1) +C t=argch(x−1) =ln(x−1+(√((x−1)^2 −1))) ⇒ e^t =x−1+(√((x−1)^2 −1)) ⇒e^(2t) =(x−1+(√((x−1)^2 −1)))^2 ⇒ I =ln(1+(x−1+(√((x−1)^2 −1)))^2 ) +C

$$\mathrm{I}=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}}}\:\Rightarrow\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{1}\right)\sqrt{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\mathrm{we}\:\mathrm{do}\:\mathrm{tbe}\:\mathrm{changement}\:\mathrm{x}−\mathrm{1}\:=\mathrm{ch}\left(\mathrm{t}\right)\:\Rightarrow\mathrm{I}\:=\int\:\:\frac{\mathrm{sh}\left(\mathrm{t}\right)\mathrm{dt}}{\left(\mathrm{ch}\left(\mathrm{t}\right).\mathrm{sht}\right.}\mathrm{dt} \\ $$$$=\int\:\:\:\frac{\mathrm{2}}{\mathrm{e}^{\mathrm{t}} \:+\mathrm{e}^{−\mathrm{t}} }\mathrm{dt}\:\:=_{\mathrm{e}^{\mathrm{t}} \:=\mathrm{u}} \:\:\mathrm{2}\:\:\int\:\:\:\:\frac{\mathrm{1}}{\mathrm{u}+\mathrm{u}^{−\mathrm{1}} }\frac{\mathrm{du}}{\mathrm{u}} \\ $$$$=\int\:\frac{\mathrm{2du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\:=\mathrm{ln}\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}\right)\:+\mathrm{C}\:=\mathrm{ln}\left(\mathrm{e}^{\mathrm{2t}} \:+\mathrm{1}\right)\:+\mathrm{C} \\ $$$$\mathrm{t}=\mathrm{argch}\left(\mathrm{x}−\mathrm{1}\right)\:=\mathrm{ln}\left(\mathrm{x}−\mathrm{1}+\sqrt{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}\right)\:\Rightarrow \\ $$$$\mathrm{e}^{\mathrm{t}} \:=\mathrm{x}−\mathrm{1}+\sqrt{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}\:\Rightarrow\mathrm{e}^{\mathrm{2t}} \:=\left(\mathrm{x}−\mathrm{1}+\sqrt{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{ln}\left(\mathrm{1}+\left(\mathrm{x}−\mathrm{1}+\sqrt{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} \right)\:+\mathrm{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com