
Question Number 122838 by bemath last updated on 20/Nov/20
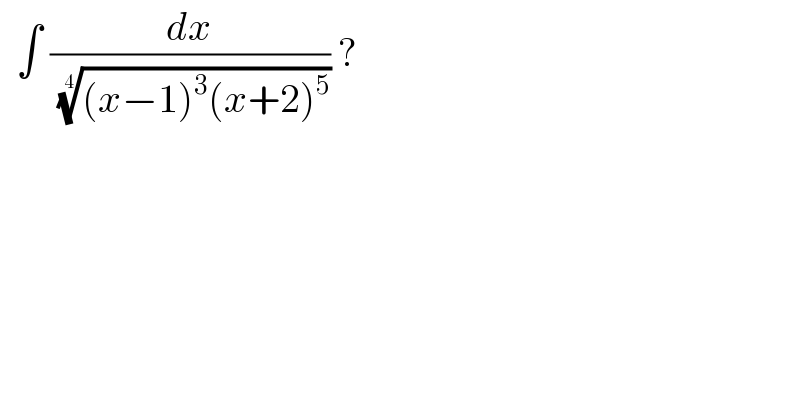
$$\:\:\int\:\frac{{dx}}{\:\sqrt[{\mathrm{4}}]{\left({x}−\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{2}\right)^{\mathrm{5}} }}\:? \\ $$
Answered by liberty last updated on 20/Nov/20

$$\:{because}\:\sqrt[{\mathrm{4}}]{\left({x}−\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{2}\right)^{\mathrm{5}} }\:=\:\left({x}−\mathrm{1}\right)\left({x}+\mathrm{2}\right)\:\sqrt[{\mathrm{4}}]{\frac{{x}+\mathrm{2}}{{x}−\mathrm{1}}} \\ $$$$\:{let}\:{u}\:=\:\sqrt[{\mathrm{4}}]{\frac{{x}+\mathrm{2}}{{x}−\mathrm{1}}}\:\Rightarrow\:{x}\:=\:\frac{{u}^{\mathrm{4}} +\mathrm{2}}{{u}^{\mathrm{4}} −\mathrm{1}} \\ $$$$\:\begin{cases}{{x}−\mathrm{1}=\frac{\mathrm{3}}{{u}^{\mathrm{4}} −\mathrm{1}}}\\{{x}+\mathrm{2}=\frac{\mathrm{3}{u}^{\mathrm{4}} }{{u}^{\mathrm{4}} −\mathrm{1}}}\end{cases}\:{and}\:{dx}\:=\:\frac{−\mathrm{12}{u}^{\mathrm{3}} }{\left({u}^{\mathrm{4}} −\mathrm{1}\right)^{\mathrm{2}} }\:{du} \\ $$$${L}\left({x}\right)=−\int\:\frac{\left({u}^{\mathrm{4}} −\mathrm{1}\right)^{\mathrm{2}} .\mathrm{12}{u}^{\mathrm{3}} }{\mathrm{3}.\mathrm{3}{u}^{\mathrm{4}} \left({u}^{\mathrm{4}} −\mathrm{1}\right)^{\mathrm{2}} {u}}\:{du}\: \\ $$$${L}\left({x}\right)=−\frac{\mathrm{4}}{\mathrm{3}}\int\:\frac{{du}}{{u}^{\mathrm{2}} }\:=\:\frac{\mathrm{4}}{\mathrm{3}{u}}\:+\:{c} \\ $$$${L}\left({x}\right)=\:\frac{\mathrm{4}}{\mathrm{3}}\sqrt[{\mathrm{4}}]{\frac{{x}−\mathrm{1}}{{x}+\mathrm{2}}}\:+\:{c}.\: \\ $$
Commented by bemath last updated on 20/Nov/20

$${great} \\ $$
