
Question Number 114102 by bemath last updated on 17/Sep/20
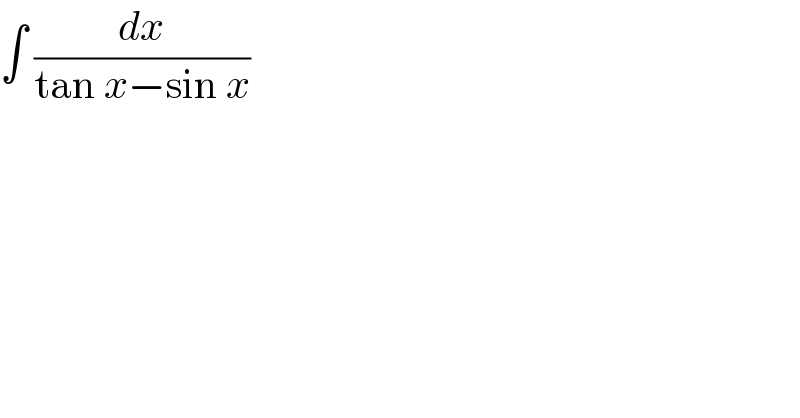
$$\int\:\frac{{dx}}{\mathrm{tan}\:{x}−\mathrm{sin}\:{x}} \\ $$
Answered by bobhans last updated on 17/Sep/20
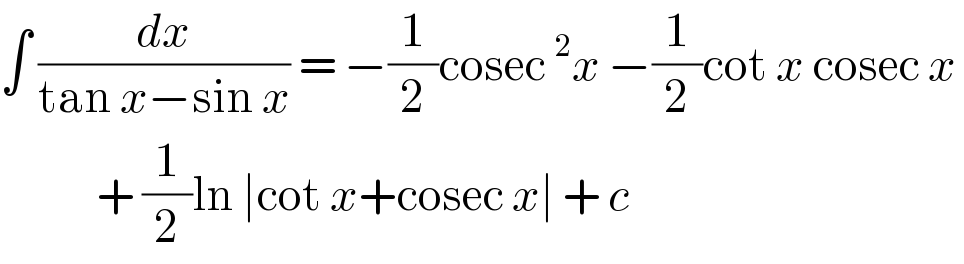
$$\int\:\frac{{dx}}{\mathrm{tan}\:{x}−\mathrm{sin}\:{x}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cosec}\:^{\mathrm{2}} {x}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cot}\:{x}\:\mathrm{cosec}\:{x}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{cot}\:{x}+\mathrm{cosec}\:{x}\mid\:+\:{c} \\ $$
Answered by 1549442205PVT last updated on 17/Sep/20
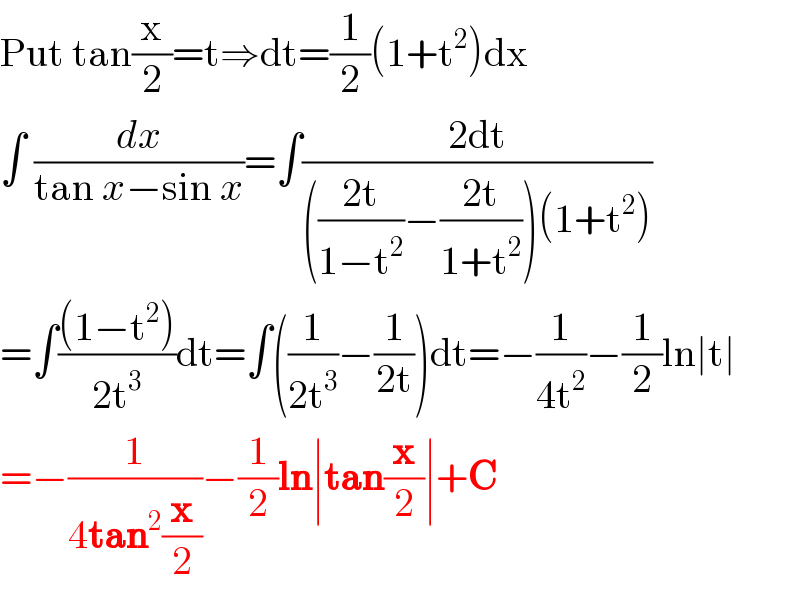
$$\mathrm{Put}\:\mathrm{tan}\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{t}\Rightarrow\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\int\:\frac{{dx}}{\mathrm{tan}\:{x}−\mathrm{sin}\:{x}}=\int\frac{\mathrm{2dt}}{\left(\frac{\mathrm{2t}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }−\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)} \\ $$$$=\int\frac{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{2t}^{\mathrm{3}} }\mathrm{dt}=\int\left(\frac{\mathrm{1}}{\mathrm{2t}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{2t}}\right)\mathrm{dt}=−\frac{\mathrm{1}}{\mathrm{4t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{t}\mid \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}\boldsymbol{\mathrm{tan}}^{\mathrm{2}} \frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{ln}}\mid\boldsymbol{\mathrm{tan}}\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}\mid+\boldsymbol{\mathrm{C}} \\ $$
