
Question Number 44148 by LXZ last updated on 22/Sep/18
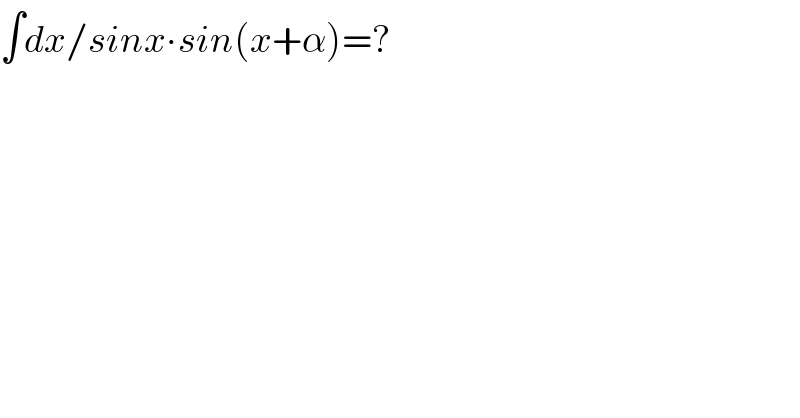
$$\int{dx}/{sinx}\centerdot{sin}\left({x}+\alpha\right)=? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Sep/18
![∫(dx/(sinx.sin(x+α))) (1/(sinα))∫((sin{(x+α)−x})/(sinx.sin(x+α)))dx (1/(sinα))∫((sin(x+α)cosx−cos(x+α)sinx)/(sinxsin(x+α)))dx (1/(sinα))[∫cotx−cot(x+α)]dx (1/(sinα))[lnsinx−lnsin(x+α)] (1/(sinα))ln{((sinx)/(sin(x+α)))}+c](Q44151.png)
$$\int\frac{{dx}}{{sinx}.{sin}\left({x}+\alpha\right)} \\ $$$$\frac{\mathrm{1}}{{sin}\alpha}\int\frac{{sin}\left\{\left({x}+\alpha\right)−{x}\right\}}{{sinx}.{sin}\left({x}+\alpha\right)}{dx} \\ $$$$\frac{\mathrm{1}}{{sin}\alpha}\int\frac{{sin}\left({x}+\alpha\right){cosx}−{cos}\left({x}+\alpha\right){sinx}}{{sinxsin}\left({x}+\alpha\right)}{dx} \\ $$$$\frac{\mathrm{1}}{{sin}\alpha}\left[\int{cotx}−{cot}\left({x}+\alpha\right)\right]{dx} \\ $$$$\frac{\mathrm{1}}{{sin}\alpha}\left[{lnsinx}−{lnsin}\left({x}+\alpha\right)\right] \\ $$$$\frac{\mathrm{1}}{{sin}\alpha}{ln}\left\{\frac{{sinx}}{{sin}\left({x}+\alpha\right)}\right\}+{c} \\ $$
