Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 177194 by peter frank last updated on 02/Oct/22

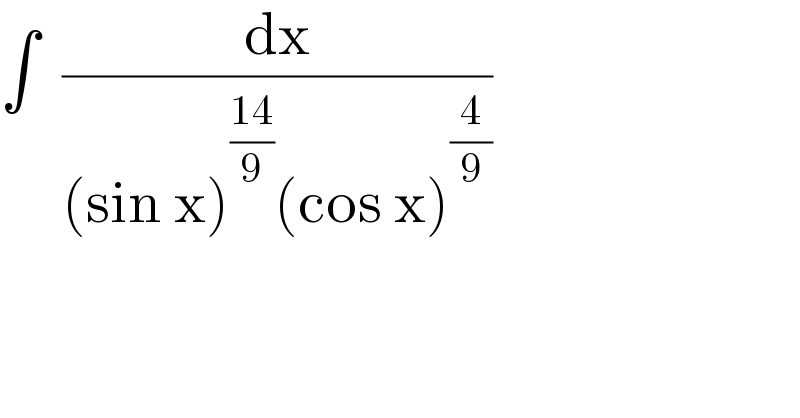
∫ (dx/((sin x)^((14)/9) (cos x)^(4/9) ))

$$\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{sin}\:\mathrm{x}\right)^{\frac{\mathrm{14}}{\mathrm{9}}} \left(\mathrm{cos}\:\mathrm{x}\right)^{\frac{\mathrm{4}}{\mathrm{9}}} } \\ $$

Answered by som(math1967) last updated on 02/Oct/22

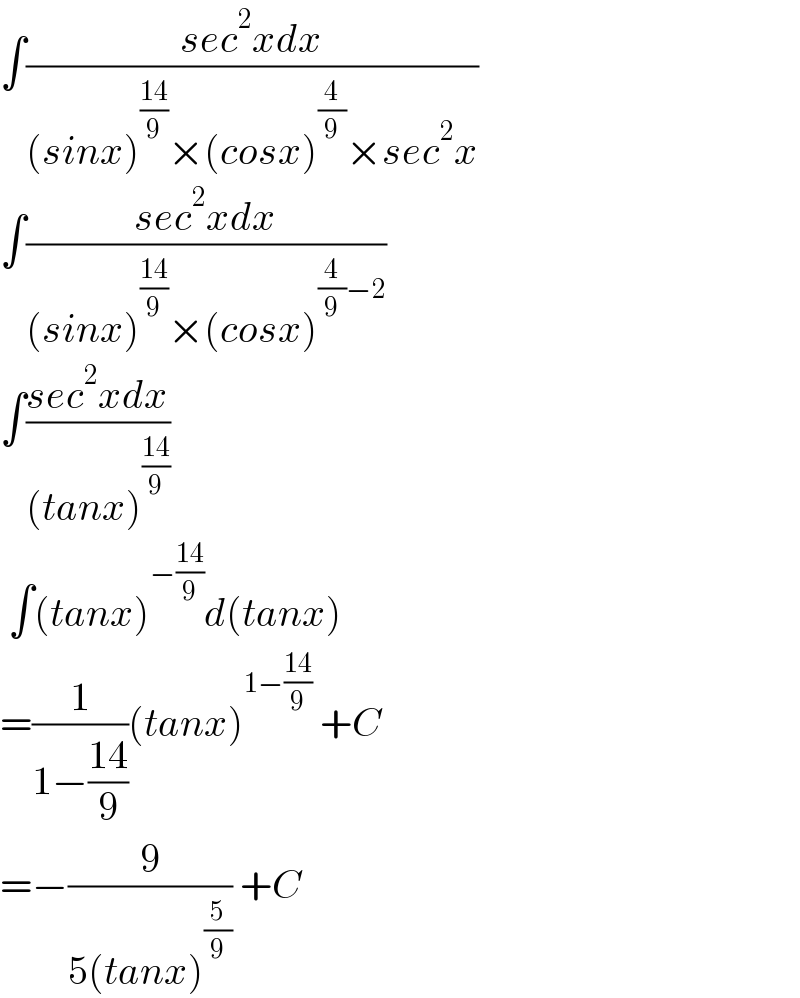
∫((sec^2 xdx)/((sinx)^((14)/9) ×(cosx)^(4/9) ×sec^2 x)) ∫((sec^2 xdx)/((sinx)^((14)/9) ×(cosx)^((4/9)−2) )) ∫((sec^2 xdx)/((tanx)^((14)/9) )) ∫(tanx)^(−((14)/9)) d(tanx) =(1/(1−((14)/9)))(tanx)^(1−((14)/9)) +C =−(9/(5(tanx)^(5/9) )) +C

$$\int\frac{{sec}^{\mathrm{2}} {xdx}}{\left({sinx}\right)^{\frac{\mathrm{14}}{\mathrm{9}}} ×\left({cosx}\right)^{\frac{\mathrm{4}}{\mathrm{9}}} ×{sec}^{\mathrm{2}} {x}} \\ $$$$\int\frac{{sec}^{\mathrm{2}} {xdx}}{\left({sinx}\right)^{\frac{\mathrm{14}}{\mathrm{9}}} ×\left({cosx}\right)^{\frac{\mathrm{4}}{\mathrm{9}}−\mathrm{2}} } \\ $$$$\int\frac{{sec}^{\mathrm{2}} {xdx}}{\left({tanx}\right)^{\frac{\mathrm{14}}{\mathrm{9}}} } \\ $$$$\:\int\left({tanx}\right)^{−\frac{\mathrm{14}}{\mathrm{9}}} {d}\left({tanx}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{14}}{\mathrm{9}}}\left({tanx}\right)^{\mathrm{1}−\frac{\mathrm{14}}{\mathrm{9}}} \:+{C} \\ $$$$=−\frac{\mathrm{9}}{\mathrm{5}\left({tanx}\right)^{\frac{\mathrm{5}}{\mathrm{9}}} }\:+{C} \\ $$

Commented by peter frank last updated on 02/Oct/22

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com