
Question Number 60311 by aliesam last updated on 19/May/19
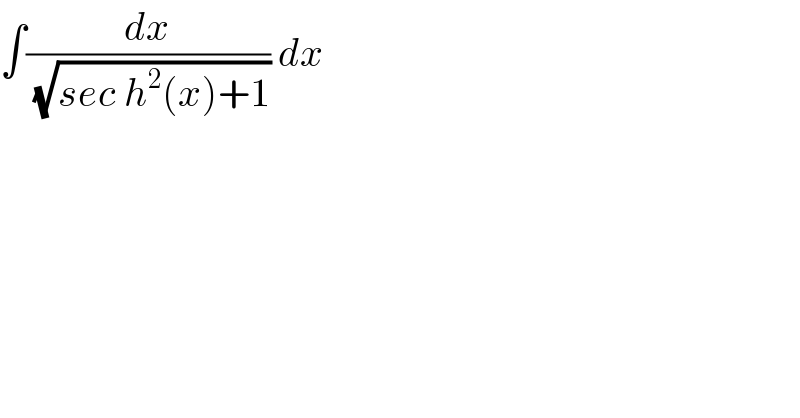
$$\int\frac{{dx}}{\sqrt{{sec}\:{h}^{\mathrm{2}} \left({x}\right)+\mathrm{1}}}\:{dx} \\ $$
Commented by MJS last updated on 20/May/19

$$\mathrm{sech}\:{x}=\frac{\mathrm{1}}{\mathrm{cosh}\:{x}} \\ $$
Commented by maxmathsup by imad last updated on 20/May/19
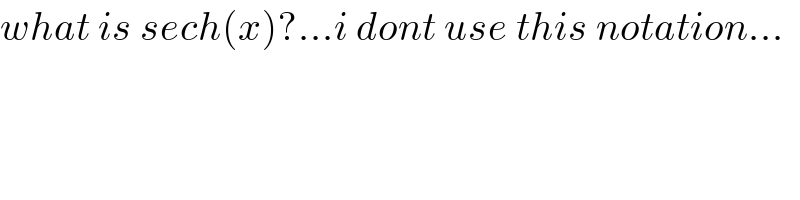
$${what}\:{is}\:{sech}\left({x}\right)?...{i}\:{dont}\:{use}\:{this}\:{notation}... \\ $$
Answered by MJS last updated on 20/May/19
![∫(dx/(√(1+sech^2 x)))=∫((cosh x)/(√(1+cosh^2 x)))dx= [t=sinh x → dx=(dt/(cosh x))] =∫(dt/(√(t^2 +2)))=ln (t+(√(t^2 +2)))= =ln (sinh x +(√(2+sinh^2 x))) +C](Q60360.png)
$$\int\frac{{dx}}{\sqrt{\mathrm{1}+\mathrm{sech}^{\mathrm{2}} \:{x}}}=\int\frac{\mathrm{cosh}\:{x}}{\sqrt{\mathrm{1}+\mathrm{cosh}^{\mathrm{2}} \:{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{sinh}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{cosh}\:{x}}\right] \\ $$$$=\int\frac{{dt}}{\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}}=\mathrm{ln}\:\left({t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}\right)= \\ $$$$=\mathrm{ln}\:\left(\mathrm{sinh}\:{x}\:+\sqrt{\mathrm{2}+\mathrm{sinh}^{\mathrm{2}} \:{x}}\right)\:+{C} \\ $$
Commented by aliesam last updated on 20/May/19
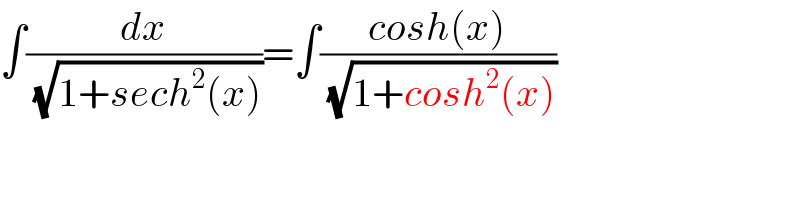
$$\int\frac{{dx}}{\sqrt{\mathrm{1}+{sech}^{\mathrm{2}} \left({x}\right)}}=\int\frac{{cosh}\left({x}\right)}{\sqrt{\mathrm{1}+{cosh}^{\mathrm{2}} \left({x}\right)}} \\ $$
Commented by MJS last updated on 20/May/19
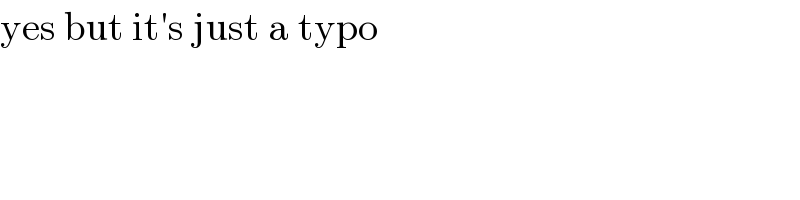
$$\mathrm{yes}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{a}\:\mathrm{typo} \\ $$
Commented by aliesam last updated on 20/May/19
$${yes}.{thank}\:{you}\:{zir} \\ $$
