
Question Number 81739 by TANMAY PANACEA last updated on 15/Feb/20
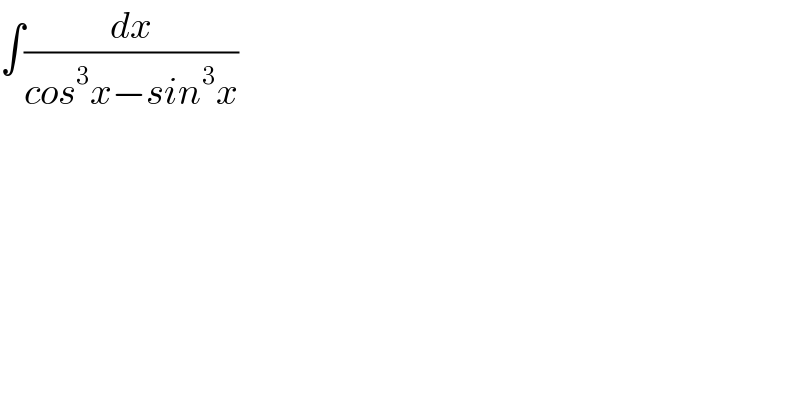
$$\int\frac{{dx}}{{cos}^{\mathrm{3}} {x}−{sin}^{\mathrm{3}} {x}} \\ $$
Commented by abdomathmax last updated on 16/Feb/20

$${I}\:=\int\:\:\frac{{dx}}{{cos}^{\mathrm{3}} {x}−{sin}^{\mathrm{3}} {x}}\:=\int\:\frac{{dx}}{\left({cosx}−{sinx}\right)\left({cos}^{\mathrm{2}} {x}\:+{cosxsinx}+{sin}^{\mathrm{2}} {x}\right)} \\ $$$$=\int\:\:\:\:\:\frac{{dx}}{\left({cosx}\:−{sinx}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{x}\right)\right)} \\ $$$$=\int\:\:\:\frac{\mathrm{2}{dx}}{\sqrt{\mathrm{2}}{sin}\left({x}−\frac{\pi}{\mathrm{4}}\right)\left(\mathrm{2}+{sin}\left(\mathrm{2}{x}\right)\right)} \\ $$$$=_{{x}−\frac{\pi}{\mathrm{4}}={t}} \:\:\sqrt{\mathrm{2}}\int\:\:\:\:\frac{{dt}}{{sin}\left({t}\right)\left(\mathrm{2}+{sin}\left(\mathrm{2}\left({t}+\frac{\pi}{\mathrm{4}}\right)\right.\right.} \\ $$$$=\sqrt{\mathrm{2}}\int\:\:\:\frac{{dt}}{{sint}\left(\mathrm{2}+{cos}\left(\mathrm{2}{t}\right)\right.}\:=\sqrt{\mathrm{2}}\int\:\:\:\frac{{dt}}{{sint}\left(\mathrm{2}+\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {t}\right)} \\ $$$$=\sqrt{\mathrm{2}}\int\:\:\:\:\frac{{dt}}{{sint}\left(\mathrm{3}−\mathrm{2}{sin}^{\mathrm{2}} {t}\right)} \\ $$$${let}\:{decompose}\:{F}\left({x}\right)\:=\frac{\mathrm{1}}{{x}\left(\mathrm{3}−\mathrm{2}{x}^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{{x}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}{x}\right)\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}{x}\right)} \\ $$$$=\frac{{a}}{{x}}\:+\frac{{b}}{\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}{x}}\:+\frac{{c}}{\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}{x}} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${b}=\frac{\sqrt{\mathrm{2}}}{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}×\frac{\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}\right)}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{6}} \\ $$$${c}=−\frac{\sqrt{\mathrm{2}}}{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\left(−\frac{\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}\right)\right)}\:=−\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}\:\Rightarrow \\ $$$$\Rightarrow\:{I}\:=\sqrt{\mathrm{2}}\int\:{F}\left({sint}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{{dt}}{{sint}}\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}\int\:\:\frac{{dt}}{\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}{sint}} \\ $$$$−\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}\int\:\:\frac{{dt}}{\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}{sint}}\:\:{integral}\:{simple}\:{to}\:{find}\:{by} \\ $$$${using}\:{changement}\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u} \\ $$
Answered by MJS last updated on 15/Feb/20
![∫(dx/(cos^3 x −sin^3 x))= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =−2∫(((t^2 +1)^2 )/((t^2 +2t−1)(t^2 −(1+(√3))t+2+(√3))(t^2 −(1−(√3))t+2−(√3))))dt= =−(4/3)∫(dt/(t^2 +2t−1))−((1+(√3))/3)∫(dt/(t^2 −(1+(√3))t+2+(√3)))−((1−(√3))/3)∫(dt/(t^2 −(1−(√3))t+2−(√3))) now use formula](Q81747.png)
$$\int\frac{{dx}}{\mathrm{cos}^{\mathrm{3}} \:{x}\:−\mathrm{sin}^{\mathrm{3}} \:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=−\mathrm{2}\int\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{2}+\sqrt{\mathrm{3}}\right)\left({t}^{\mathrm{2}} −\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}+\mathrm{2}−\sqrt{\mathrm{3}}\right)}{dt}= \\ $$$$=−\frac{\mathrm{4}}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}}−\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{2}+\sqrt{\mathrm{3}}}−\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}+\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$$\mathrm{now}\:\mathrm{use}\:\mathrm{formula} \\ $$
Commented by TANMAY PANACEA last updated on 15/Feb/20

$${excellent}\:{sir} \\ $$
Answered by TANMAY PANACEA last updated on 15/Feb/20
![∫(dx/((cosx−sinx)(1+sinxcosx))) ∫(((cosx−sinx)^2 +2sinxcosx+2−2)/((cosx−sinx)(1+cosxsinx)))dx ∫((cosx−sinx)/((1/2)[1+(sinx+cosx)^2 ]))dx+∫((2dx)/(cosx−sinx))−2I I=(2/3)∫((d(sinx+cosx))/(1+(sinx+cosx)^2 ))+(2/3)∫((1/(√2))/(sin((π/4)−x))) I=(2/3)tan^(−1) (sinx+cosx)+((√2)/3)∫cosec((π/4)−x)dx I=(2/3)tan^(−1) (sinx+cosx)−((√2)/3)lntan((π/8)−(x/2))+c pls check mistake if any](Q81812.png)
$$\int\frac{{dx}}{\left({cosx}−{sinx}\right)\left(\mathrm{1}+{sinxcosx}\right)} \\ $$$$\int\frac{\left({cosx}−{sinx}\right)^{\mathrm{2}} +\mathrm{2}{sinxcosx}+\mathrm{2}−\mathrm{2}}{\left({cosx}−{sinx}\right)\left(\mathrm{1}+{cosxsinx}\right)}{dx} \\ $$$$\int\frac{{cosx}−{sinx}}{\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}+\left({sinx}+{cosx}\right)^{\mathrm{2}} \right]}{dx}+\int\frac{\mathrm{2}{dx}}{{cosx}−{sinx}}−\mathrm{2}{I} \\ $$$${I}=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{d}\left({sinx}+{cosx}\right)}{\mathrm{1}+\left({sinx}+{cosx}\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}}{{sin}\left(\frac{\pi}{\mathrm{4}}−{x}\right)} \\ $$$${I}=\frac{\mathrm{2}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left({sinx}+{cosx}\right)+\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\int{cosec}\left(\frac{\pi}{\mathrm{4}}−{x}\right){dx} \\ $$$${I}=\frac{\mathrm{2}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left({sinx}+{cosx}\right)−\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}{lntan}\left(\frac{\pi}{\mathrm{8}}−\frac{{x}}{\mathrm{2}}\right)+{c} \\ $$$${pls}\:{check}\:{mistake}\:{if}\:{any} \\ $$
