
Question Number 87103 by hamdhan last updated on 02/Apr/20
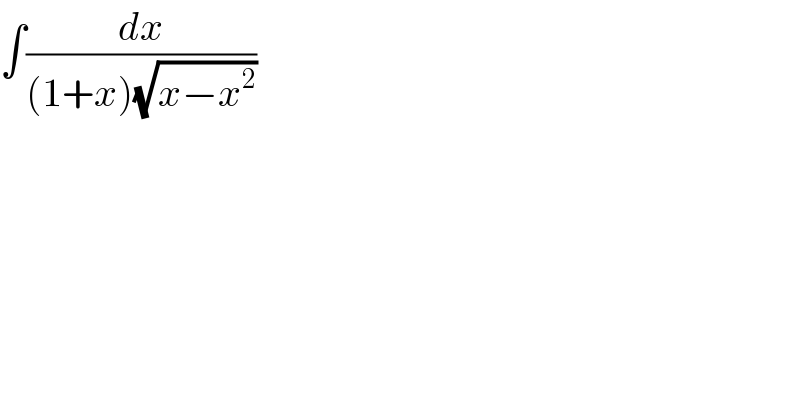
$$\int\frac{{dx}}{\left(\mathrm{1}+{x}\right)\sqrt{{x}−{x}^{\mathrm{2}} }} \\ $$
Commented by abdomathmax last updated on 02/Apr/20

$${I}\:=\int\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{−\left({x}^{\mathrm{2}} −{x}\right)}}\:=\int\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{−\left({x}^{\mathrm{2}} −{x}\:+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}\right)}} \\ $$$$=\int\:\:\:\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{\frac{\mathrm{1}}{\mathrm{4}}−\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }}\:{changement} \\ $$$${x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}{sint}\:{give} \\ $$$${I}\:=\int\:\:\:\:\:\:\frac{{cost}\:{dt}}{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{sint}\right)\frac{\mathrm{1}}{\mathrm{2}}{cost}} \\ $$$$=\int\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{sint}}\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}} \:\:\:\:\mathrm{2}\:\int\:\:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{4}\:\int\:\:\:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} \:+\mathrm{2}{u}}\:=\mathrm{4}\:\int\:\:\frac{{du}}{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }\:=−\frac{\mathrm{4}}{\mathrm{1}+{u}}\:+{C} \\ $$$$=−\frac{\mathrm{4}}{\mathrm{1}+{tan}\left(\frac{{t}}{\mathrm{2}}\right)}\:+{C} \\ $$$${t}\:={arcsin}\left(\mathrm{2}{x}−\mathrm{1}\right)\:\Rightarrow \\ $$$${I}\:\:=\frac{−\mathrm{4}}{\mathrm{1}+{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsin}\left(\mathrm{2}{x}−\mathrm{1}\right)\right)}\:+{C} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 02/Apr/20

$${Nice} \\ $$
Answered by hamdhan last updated on 02/Apr/20
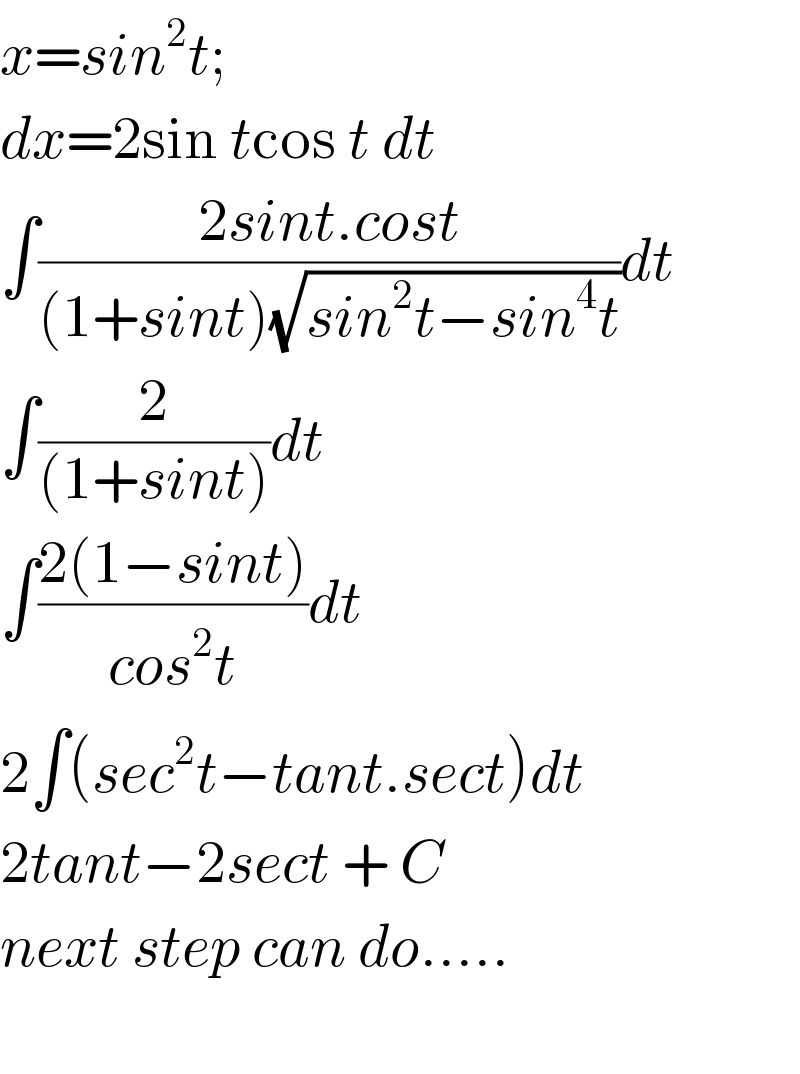
$${x}={sin}^{\mathrm{2}} {t}; \\ $$$${dx}=\mathrm{2sin}\:{t}\mathrm{cos}\:{t}\:{dt} \\ $$$$\int\frac{\mathrm{2}{sint}.{cost}}{\left(\mathrm{1}+{sint}\right)\sqrt{{sin}^{\mathrm{2}} {t}−{sin}^{\mathrm{4}} {t}}}{dt} \\ $$$$\int\frac{\mathrm{2}}{\left(\mathrm{1}+{sint}\right)}{dt} \\ $$$$\int\frac{\mathrm{2}\left(\mathrm{1}−{sint}\right)}{{cos}^{\mathrm{2}} {t}}{dt} \\ $$$$\mathrm{2}\int\left({sec}^{\mathrm{2}} {t}−{tant}.{sect}\right){dt} \\ $$$$\mathrm{2}{tant}−\mathrm{2}{sect}\:+\:{C} \\ $$$${next}\:{step}\:{can}\:{do}..... \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 04/Apr/20
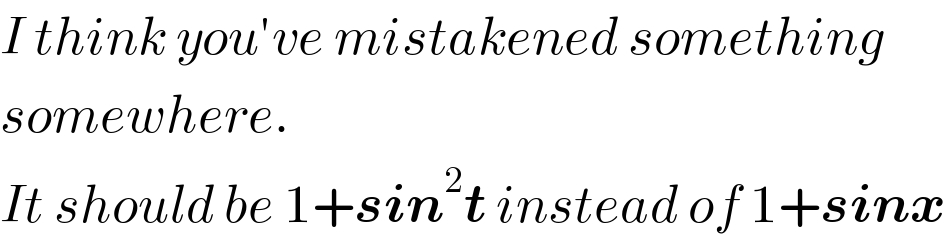
$${I}\:{think}\:{you}'{ve}\:{mistakened}\:{something} \\ $$$${somewhere}. \\ $$$${It}\:{should}\:{be}\:\mathrm{1}+\boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{{t}}\:{instead}\:{of}\:\mathrm{1}+\boldsymbol{{sinx}} \\ $$
Answered by MJS last updated on 02/Apr/20
![without trigonometric substitution: ∫(dx/((1+x)(√(x−x^2 ))))=∫(dx/((1+x)(√(x(1−x))))) [t=(√((1−x)/x)) → dx=−2(√(x^3 (1−x)))dt] =−2∫(dt/(t^2 +2))=−(√2)arctan (t/(√3)) = =−(√2)arctan (√((1−x)/(2x))) +C](Q87112.png)
$$\mathrm{without}\:\mathrm{trigonometric}\:\mathrm{substitution}: \\ $$$$\int\frac{{dx}}{\left(\mathrm{1}+{x}\right)\sqrt{{x}−{x}^{\mathrm{2}} }}=\int\frac{{dx}}{\left(\mathrm{1}+{x}\right)\sqrt{{x}\left(\mathrm{1}−{x}\right)}} \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\frac{\mathrm{1}−{x}}{{x}}}\:\rightarrow\:{dx}=−\mathrm{2}\sqrt{{x}^{\mathrm{3}} \left(\mathrm{1}−{x}\right)}{dt}\right] \\ $$$$=−\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}}=−\sqrt{\mathrm{2}}\mathrm{arctan}\:\frac{{t}}{\sqrt{\mathrm{3}}}\:= \\ $$$$=−\sqrt{\mathrm{2}}\mathrm{arctan}\:\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{2}{x}}}\:+{C} \\ $$
Commented by john santu last updated on 03/Apr/20

$$\mathrm{super}....\mathrm{sir} \\ $$
