Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 145324 by mathdanisur last updated on 04/Jul/21

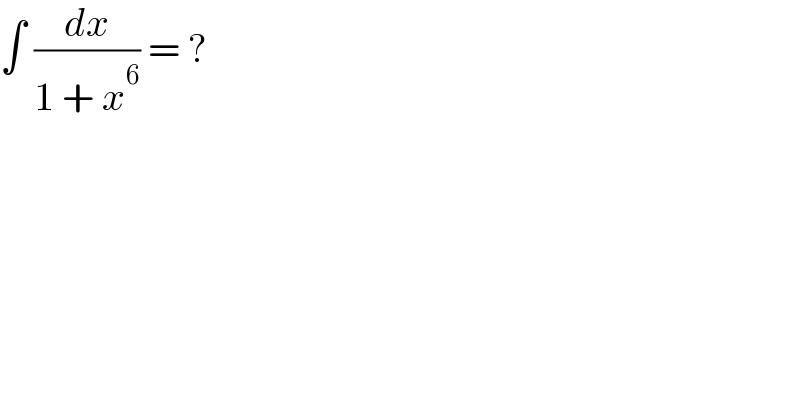
∫ (dx/(1 + x^6 )) = ?

$$\int\:\frac{{dx}}{\mathrm{1}\:+\:{x}^{\mathrm{6}} }\:=\:? \\ $$

Answered by Olaf_Thorendsen last updated on 04/Jul/21

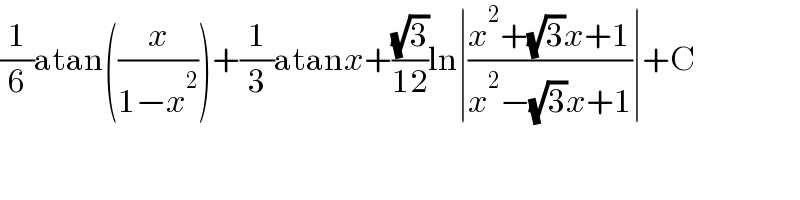
(1/6)atan((x/(1−x^2 )))+(1/3)atanx+((√3)/(12))ln∣((x^2 +(√3)x+1)/(x^2 −(√3)x+1))∣+C

$$\frac{\mathrm{1}}{\mathrm{6}}\mathrm{atan}\left(\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\right)+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{atan}{x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\mathrm{ln}\mid\frac{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}\mid+\mathrm{C} \\ $$

Commented by mathdanisur last updated on 04/Jul/21

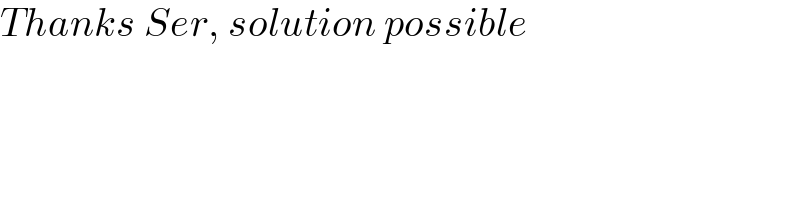
Thanks Ser, solution possible

$${Thanks}\:{Ser},\:{solution}\:{possible} \\ $$

Answered by Canebulok last updated on 04/Jul/21

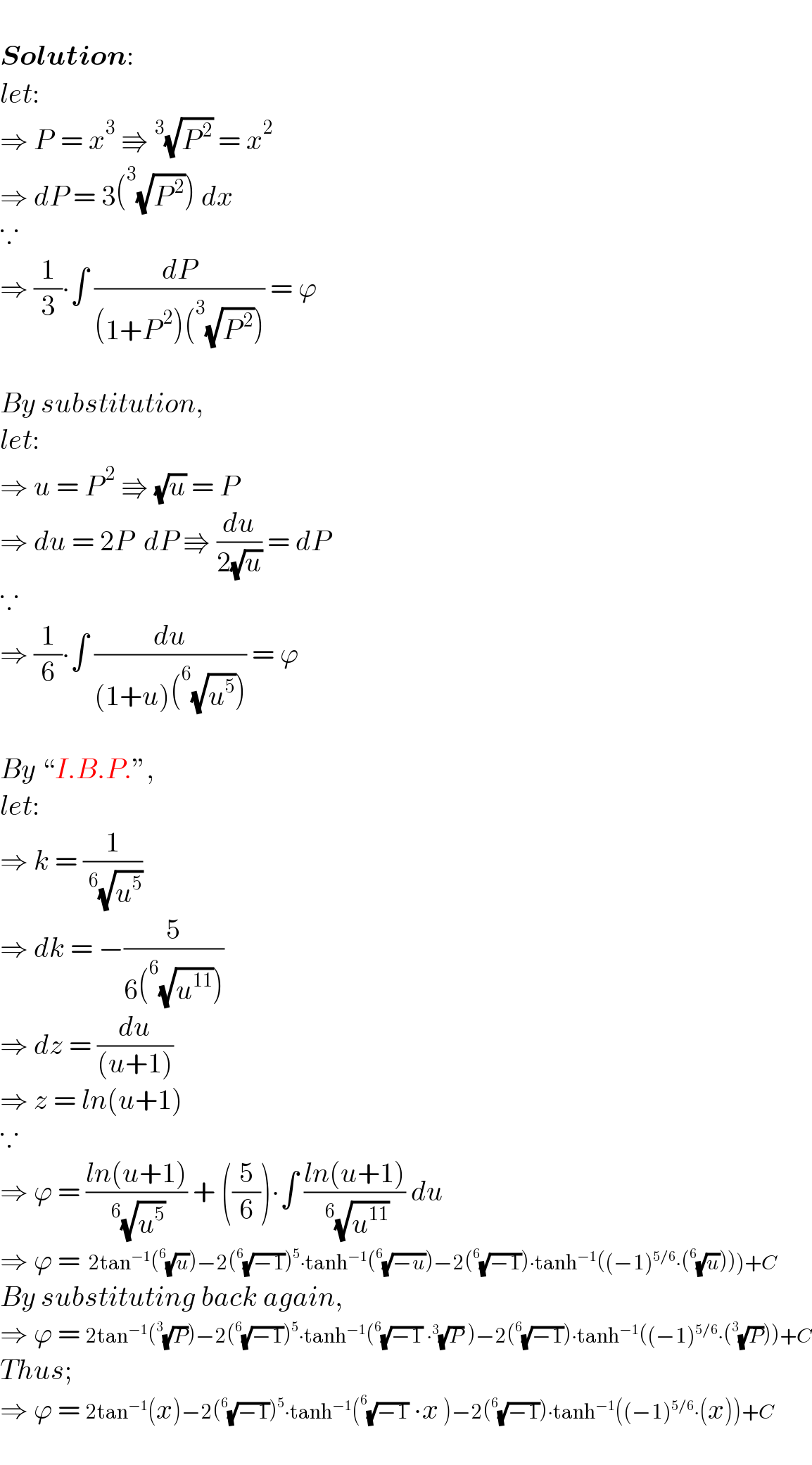
Solution: let: ⇒ P^ = x^3 ⇛^3 (√P^( 2) ) = x^2 ⇒ dP = 3(^3 (√P^( 2) )) dx ∵ ⇒ (1/3)∙∫ (dP/((1+P^( 2) )(^3 (√P^( 2) )))) = ϕ By substitution, let: ⇒ u = P^( 2) ⇛ (√u) = P ⇒ du = 2P dP ⇛ (du/(2(√u))) = dP ∵ ⇒ (1/6)∙∫ (du/((1+u)(^6 (√u^5 )))) = ϕ By “I.B.P.”, let: ⇒ k = (1/(^6 (√u^5 ))) ⇒ dk = −(5/(6(^6 (√u^(11) )))) ⇒ dz = (du/((u+1))) ⇒ z = ln(u+1) ∵ ⇒ ϕ = ((ln(u+1))/(^6 (√u^5 ))) + ((5/6))∙∫ ((ln(u+1))/(^6 (√u^(11) ))) du ⇒ ϕ = 2tan^(−1) (^6 (√u))−2(^6 (√(−1)))^5 ∙tanh^(−1) (^6 (√(−u)))−2(^6 (√(−1)))∙tanh^(−1) ((−1)^(5/6) ∙(^6 (√u))))+C By substituting back again, ⇒ ϕ = 2tan^(−1) (^3 (√P))−2(^6 (√(−1)))^5 ∙tanh^(−1) (^6 (√(−1)) ∙^3 (√P) )−2(^6 (√(−1)))∙tanh^(−1) ((−1)^(5/6) ∙(^3 (√P)))+C Thus; ⇒ ϕ = 2tan^(−1) (x)−2(^6 (√(−1)))^5 ∙tanh^(−1) (^6 (√(−1)) ∙x )−2(^6 (√(−1)))∙tanh^(−1) ((−1)^(5/6) ∙(x))+C

$$\: \\ $$$$\boldsymbol{{Solution}}: \\ $$$${let}: \\ $$$$\Rightarrow\:{P}^{\:} \:=\:{x}^{\mathrm{3}} \:\Rrightarrow\:^{\mathrm{3}} \sqrt{{P}^{\:\mathrm{2}} }\:=\:{x}^{\mathrm{2}} \\ $$$$\Rightarrow\:{dP}\:=\:\mathrm{3}\left(^{\mathrm{3}} \sqrt{{P}^{\:\mathrm{2}} }\right)\:{dx} \\ $$$$\because \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{3}}\centerdot\int\:\frac{{dP}}{\left(\mathrm{1}+{P}^{\:\mathrm{2}} \right)\left(^{\mathrm{3}} \sqrt{{P}^{\:\mathrm{2}} }\right)}\:=\:\varphi \\ $$$$\: \\ $$$${By}\:{substitution}, \\ $$$${let}: \\ $$$$\Rightarrow\:{u}\:=\:{P}^{\:\mathrm{2}} \:\Rrightarrow\:\sqrt{{u}}\:=\:{P} \\ $$$$\Rightarrow\:{du}\:=\:\mathrm{2}{P}\:\:{dP}\:\Rrightarrow\:\frac{{du}}{\mathrm{2}\sqrt{{u}}}\:=\:{dP} \\ $$$$\because \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{6}}\centerdot\int\:\frac{{du}}{\left(\mathrm{1}+{u}\right)\left(^{\mathrm{6}} \sqrt{{u}^{\mathrm{5}} }\right)}\:=\:\varphi \\ $$$$\: \\ $$$${By}\:``{I}.{B}.{P}.'', \\ $$$${let}: \\ $$$$\Rightarrow\:{k}\:=\:\frac{\mathrm{1}}{\:^{\mathrm{6}} \sqrt{{u}^{\mathrm{5}} }} \\ $$$$\Rightarrow\:{dk}\:=\:−\frac{\mathrm{5}}{\mathrm{6}\left(^{\mathrm{6}} \sqrt{{u}^{\mathrm{11}} }\right)} \\ $$$$\Rightarrow\:{dz}\:=\:\frac{{du}}{\left({u}+\mathrm{1}\right)} \\ $$$$\Rightarrow\:{z}\:=\:{ln}\left({u}+\mathrm{1}\right) \\ $$$$\because \\ $$$$\Rightarrow\:\varphi\:=\:\frac{{ln}\left({u}+\mathrm{1}\right)}{\:^{\mathrm{6}} \sqrt{{u}^{\mathrm{5}} }}\:+\:\left(\frac{\mathrm{5}}{\mathrm{6}}\right)\centerdot\int\:\frac{{ln}\left({u}+\mathrm{1}\right)}{\:^{\mathrm{6}} \sqrt{{u}^{\mathrm{11}} }}\:{du} \\ $$$$\left.\Rightarrow\:\varphi\:=\:\:\mathrm{2tan}^{−\mathrm{1}} \left(^{\mathrm{6}} \sqrt{{u}}\right)−\mathrm{2}\left(^{\mathrm{6}} \sqrt{−\mathrm{1}}\right)^{\mathrm{5}} \centerdot\mathrm{tanh}^{−\mathrm{1}} \left(^{\mathrm{6}} \sqrt{−{u}}\right)−\mathrm{2}\left(^{\mathrm{6}} \sqrt{−\mathrm{1}}\right)\centerdot\mathrm{tanh}^{−\mathrm{1}} \left(\left(−\mathrm{1}\right)^{\mathrm{5}/\mathrm{6}} \centerdot\left(^{\mathrm{6}} \sqrt{{u}}\right)\right)\right)+{C} \\ $$$${By}\:{substituting}\:{back}\:{again}, \\ $$$$\Rightarrow\:\varphi\:=\:\mathrm{2tan}^{−\mathrm{1}} \left(^{\mathrm{3}} \sqrt{{P}}\right)−\mathrm{2}\left(^{\mathrm{6}} \sqrt{−\mathrm{1}}\right)^{\mathrm{5}} \centerdot\mathrm{tanh}^{−\mathrm{1}} \left(^{\mathrm{6}} \sqrt{−\mathrm{1}}\:\centerdot^{\mathrm{3}} \sqrt{{P}}\:\right)−\mathrm{2}\left(^{\mathrm{6}} \sqrt{−\mathrm{1}}\right)\centerdot\mathrm{tanh}^{−\mathrm{1}} \left(\left(−\mathrm{1}\right)^{\mathrm{5}/\mathrm{6}} \centerdot\left(^{\mathrm{3}} \sqrt{{P}}\right)\right)+{C} \\ $$$${Thus}; \\ $$$$\Rightarrow\:\varphi\:=\:\mathrm{2tan}^{−\mathrm{1}} \left({x}\right)−\mathrm{2}\left(^{\mathrm{6}} \sqrt{−\mathrm{1}}\right)^{\mathrm{5}} \centerdot\mathrm{tanh}^{−\mathrm{1}} \left(^{\mathrm{6}} \sqrt{−\mathrm{1}}\:\centerdot{x}\:\right)−\mathrm{2}\left(^{\mathrm{6}} \sqrt{−\mathrm{1}}\right)\centerdot\mathrm{tanh}^{−\mathrm{1}} \left(\left(−\mathrm{1}\right)^{\mathrm{5}/\mathrm{6}} \centerdot\left({x}\right)\right)+{C} \\ $$$$\: \\ $$

Commented by mathdanisur last updated on 04/Jul/21

Thanks Ser, cool alot

$${Thanks}\:{Ser},\:{cool}\:{alot} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com