
Question Number 129645 by liberty last updated on 17/Jan/21
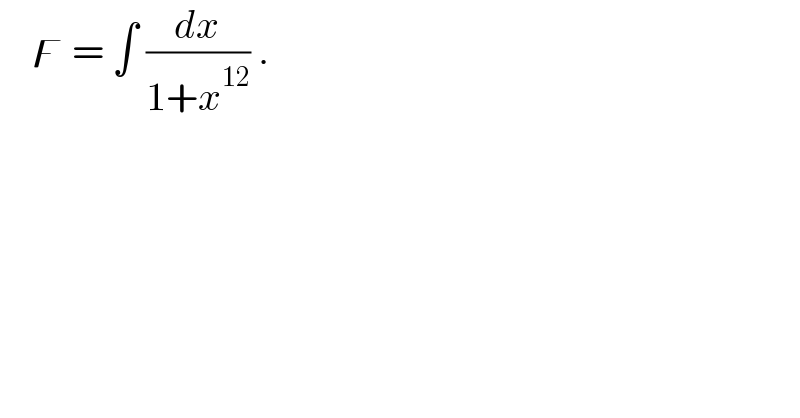
$$\:\:\:\:\digamma\:=\:\int\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{12}} }\:. \\ $$
Answered by mathmax by abdo last updated on 17/Jan/21
![roots of z^(12) +1=0 ⇒z^(12) =e^(iπ +2ikπ) =e^(i(2k+1)π) ⇒z_k =e^(i((2k+1)π)/(12))) withk∈[[0,11]] and (1/(z^(12) +1))=(1/(Π_(k=0) ^(11) (z−z_k )))=Σ_(k=0) ^(11) (a_k /(z−z_k )) a_k =(1/(12z_k ^(11) )) =(z_k /(−12)) ⇒a_k =−(1/(12))Σ_(k=0) ^(11) (z_k /(z−z_k )) ⇒ F=−(1/(12))Σ_(k=0) ^(11) z_k ∫ (dx/(x−z_k )) =−(1/(12))Σ_(k=0) ^(11) z_k ln(x−z_k ) +C](Q129670.png)
$$\mathrm{roots}\:\mathrm{of}\:\mathrm{z}^{\mathrm{12}} +\mathrm{1}=\mathrm{0}\:\:\:\Rightarrow\mathrm{z}^{\mathrm{12}} \:=\mathrm{e}^{\mathrm{i}\pi\:+\mathrm{2ik}\pi} \:=\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}+\mathrm{1}\right)\pi} \:\Rightarrow\mathrm{z}_{\mathrm{k}} =\mathrm{e}^{\mathrm{i}\frac{\left.\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{12}}} \:\:\mathrm{withk}\in\left[\left[\mathrm{0},\mathrm{11}\right]\right] \\ $$$$\mathrm{and}\:\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{12}} +\mathrm{1}}=\frac{\mathrm{1}}{\prod_{\mathrm{k}=\mathrm{0}} ^{\mathrm{11}} \left(\mathrm{z}−\mathrm{z}_{\mathrm{k}} \right)}=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{11}} \:\frac{\mathrm{a}_{\mathrm{k}} }{\mathrm{z}−\mathrm{z}_{\mathrm{k}} } \\ $$$$\mathrm{a}_{\mathrm{k}} =\frac{\mathrm{1}}{\mathrm{12z}_{\mathrm{k}} ^{\mathrm{11}} }\:=\frac{\mathrm{z}_{\mathrm{k}} }{−\mathrm{12}}\:\Rightarrow\mathrm{a}_{\mathrm{k}} =−\frac{\mathrm{1}}{\mathrm{12}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{11}} \:\frac{\mathrm{z}_{\mathrm{k}} }{\mathrm{z}−\mathrm{z}_{\mathrm{k}} }\:\Rightarrow \\ $$$$\mathrm{F}=−\frac{\mathrm{1}}{\mathrm{12}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{11}} \mathrm{z}_{\mathrm{k}} \:\int\:\:\frac{\mathrm{dx}}{\mathrm{x}−\mathrm{z}_{\mathrm{k}} }\:=−\frac{\mathrm{1}}{\mathrm{12}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{11}} \mathrm{z}_{\mathrm{k}} \mathrm{ln}\left(\mathrm{x}−\mathrm{z}_{\mathrm{k}} \right)\:+\mathrm{C} \\ $$
