
Question Number 60007 by meme last updated on 17/May/19
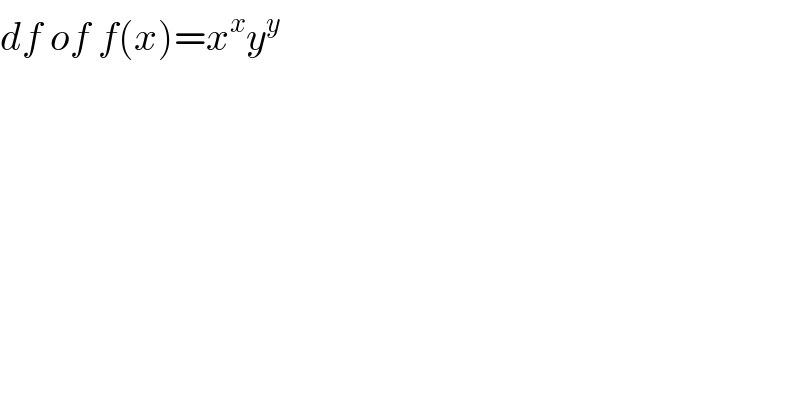
$${df}\:{of}\:{f}\left({x}\right)={x}^{{x}} {y}^{{y}} \\ $$
Answered by alex041103 last updated on 18/May/19
![if you mean f(x,y)=x^x y^y then df=(∂f/∂x)dx+(∂f/∂y)dy= =y^y (∂/∂x)(x^x )dx+x^x (∂/∂y)(y^y )dy= In general let′s find (∂/∂z)z^z : z^z =e^(z ln(z)) ⇒(∂/∂z)(z^z )=(∂/∂z)(e^(z ln(z)) )= =(∂/(∂(z ln(z))))(e^(z ln(z)) )×((∂(z ln(z)))/∂z)= =e^(z ln(z)) ×(1×ln(z)+z×(1/z))= =z^z (1+ln(z))=((∂(z^z ))/∂z) ⇒df=x^x y^y (1+ln(x))dx+x^x y^y (1+ln(y))dy ⇒df=f[(1+ln(x))dx+(1+ln(y))dy] you can go a little bit further: (df/f)=dx+ln(x)dx+dy+ln(y)dy= =d(x+y)+ln(x^dx )+ln(y^dy )= =d(x+y)+ln(x^dx y^dy ) ⇒df=x^x y^y [d(x+y)+ln(x^dx y^dy )]](Q60144.png)
$${if}\:{you}\:{mean}\:{f}\left({x},{y}\right)={x}^{{x}} {y}^{{y}} \:{then} \\ $$$${df}=\frac{\partial{f}}{\partial{x}}{dx}+\frac{\partial{f}}{\partial{y}}{dy}= \\ $$$$={y}^{{y}} \frac{\partial}{\partial{x}}\left({x}^{{x}} \right){dx}+{x}^{{x}} \frac{\partial}{\partial{y}}\left({y}^{{y}} \right){dy}= \\ $$$${In}\:{general}\:{let}'{s}\:{find}\:\frac{\partial}{\partial{z}}{z}^{{z}} : \\ $$$${z}^{{z}} ={e}^{{z}\:{ln}\left({z}\right)} \Rightarrow\frac{\partial}{\partial{z}}\left({z}^{{z}} \right)=\frac{\partial}{\partial{z}}\left({e}^{{z}\:{ln}\left({z}\right)} \right)= \\ $$$$=\frac{\partial}{\partial\left({z}\:{ln}\left({z}\right)\right)}\left({e}^{{z}\:{ln}\left({z}\right)} \right)×\frac{\partial\left({z}\:{ln}\left({z}\right)\right)}{\partial{z}}= \\ $$$$={e}^{{z}\:{ln}\left({z}\right)} ×\left(\mathrm{1}×{ln}\left({z}\right)+{z}×\frac{\mathrm{1}}{{z}}\right)= \\ $$$$={z}^{{z}} \left(\mathrm{1}+{ln}\left({z}\right)\right)=\frac{\partial\left({z}^{{z}} \right)}{\partial{z}} \\ $$$$\Rightarrow{df}={x}^{{x}} {y}^{{y}} \left(\mathrm{1}+{ln}\left({x}\right)\right){dx}+{x}^{{x}} {y}^{{y}} \left(\mathrm{1}+{ln}\left({y}\right)\right){dy} \\ $$$$\Rightarrow{df}={f}\left[\left(\mathrm{1}+{ln}\left({x}\right)\right){dx}+\left(\mathrm{1}+{ln}\left({y}\right)\right){dy}\right] \\ $$$${you}\:{can}\:{go}\:{a}\:{little}\:{bit}\:{further}: \\ $$$$\frac{{df}}{{f}}={dx}+{ln}\left({x}\right){dx}+{dy}+{ln}\left({y}\right){dy}= \\ $$$$={d}\left({x}+{y}\right)+{ln}\left({x}^{{dx}} \right)+{ln}\left({y}^{{dy}} \right)= \\ $$$$={d}\left({x}+{y}\right)+{ln}\left({x}^{{dx}} {y}^{{dy}} \right) \\ $$$$\Rightarrow{df}={x}^{{x}} {y}^{{y}} \left[{d}\left({x}+{y}\right)+{ln}\left({x}^{{dx}} {y}^{{dy}} \right)\right] \\ $$
