Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 177769 by a.lgnaoui last updated on 08/Oct/22

determiner les elements demandes dans le graphe

$${determiner}\:{les}\:{elements}\:{demandes} \\ $$$${dans}\:{le}\:{graphe} \\ $$

Commented by a.lgnaoui last updated on 08/Oct/22

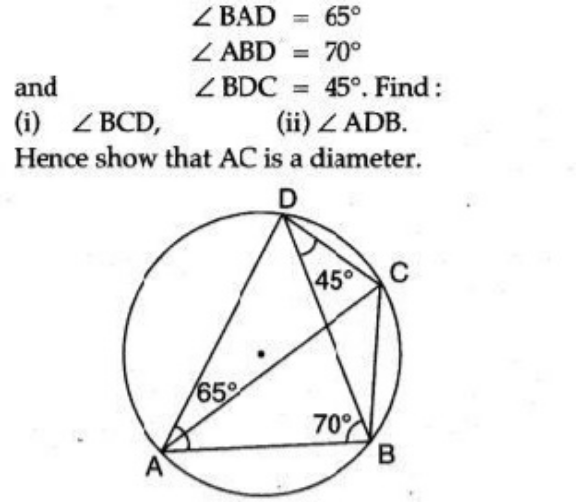
Commented by a.lgnaoui last updated on 09/Oct/22

∡ADB=180−(65+70)=45 ∡BDC=45 ⇒∡ADC=90 Donc △ADC triangle rectangle doonc AC passe par centre du cercle AC=diametre ACB aussi triangle rectangle donc ∡DBC=90−70=20 Donc ∡ BCD=180−(45+20)=115

$$\measuredangle\mathrm{ADB}=\mathrm{180}−\left(\mathrm{65}+\mathrm{70}\right)=\mathrm{45} \\ $$$$\measuredangle\mathrm{BDC}=\mathrm{45}\:\:\:\:\Rightarrow\measuredangle\mathrm{ADC}=\mathrm{90} \\ $$$$\mathrm{Donc}\:\:\:\bigtriangleup\mathrm{ADC}\:\mathrm{triangle}\:\mathrm{rectangle} \\ $$$$\mathrm{doonc}\:\:\mathrm{AC}\:\:\mathrm{passe}\:\mathrm{par}\:\mathrm{centre}\:\mathrm{du}\:\mathrm{cercle} \\ $$$$\mathrm{AC}=\mathrm{diametre}\: \\ $$$$\mathrm{ACB}\:\:\mathrm{aussi}\:\mathrm{triangle}\:\mathrm{rectangle} \\ $$$$\mathrm{donc}\:\:\measuredangle\mathrm{DBC}=\mathrm{90}−\mathrm{70}=\mathrm{20} \\ $$$$\mathrm{Donc}\:\measuredangle\:\mathrm{BCD}=\mathrm{180}−\left(\mathrm{45}+\mathrm{20}\right)=\mathrm{115} \\ $$

Answered by Ar Brandon last updated on 08/Oct/22

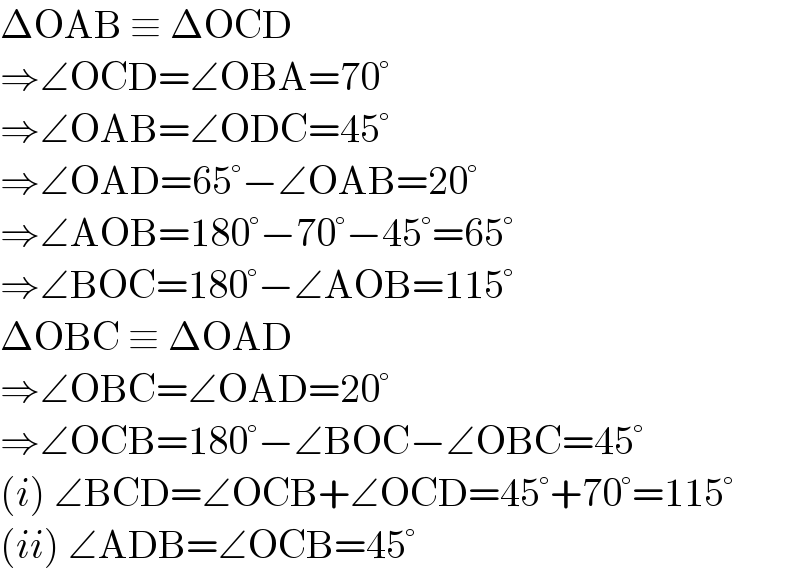
ΔOAB ≡ ΔOCD ⇒∠OCD=∠OBA=70° ⇒∠OAB=∠ODC=45° ⇒∠OAD=65°−∠OAB=20° ⇒∠AOB=180°−70°−45°=65° ⇒∠BOC=180°−∠AOB=115° ΔOBC ≡ ΔOAD ⇒∠OBC=∠OAD=20° ⇒∠OCB=180°−∠BOC−∠OBC=45° (i) ∠BCD=∠OCB+∠OCD=45°+70°=115° (ii) ∠ADB=∠OCB=45°

$$\Delta\mathrm{OAB}\:\equiv\:\Delta\mathrm{OCD}\: \\ $$$$\Rightarrow\angle\mathrm{OCD}=\angle\mathrm{OBA}=\mathrm{70}° \\ $$$$\Rightarrow\angle\mathrm{OAB}=\angle\mathrm{ODC}=\mathrm{45}° \\ $$$$\Rightarrow\angle\mathrm{OAD}=\mathrm{65}°−\angle\mathrm{OAB}=\mathrm{20}° \\ $$$$\Rightarrow\angle\mathrm{AOB}=\mathrm{180}°−\mathrm{70}°−\mathrm{45}°=\mathrm{65}° \\ $$$$\Rightarrow\angle\mathrm{BOC}=\mathrm{180}°−\angle\mathrm{AOB}=\mathrm{115}° \\ $$$$\Delta\mathrm{OBC}\:\equiv\:\Delta\mathrm{OAD} \\ $$$$\Rightarrow\angle\mathrm{OBC}=\angle\mathrm{OAD}=\mathrm{20}° \\ $$$$\Rightarrow\angle\mathrm{OCB}=\mathrm{180}°−\angle\mathrm{BOC}−\angle\mathrm{OBC}=\mathrm{45}° \\ $$$$\left({i}\right)\:\angle\mathrm{BCD}=\angle\mathrm{OCB}+\angle\mathrm{OCD}=\mathrm{45}°+\mathrm{70}°=\mathrm{115}° \\ $$$$\left({ii}\right)\:\angle\mathrm{ADB}=\angle\mathrm{OCB}=\mathrm{45}° \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com