Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 203774 by Calculusboy last updated on 27/Jan/24

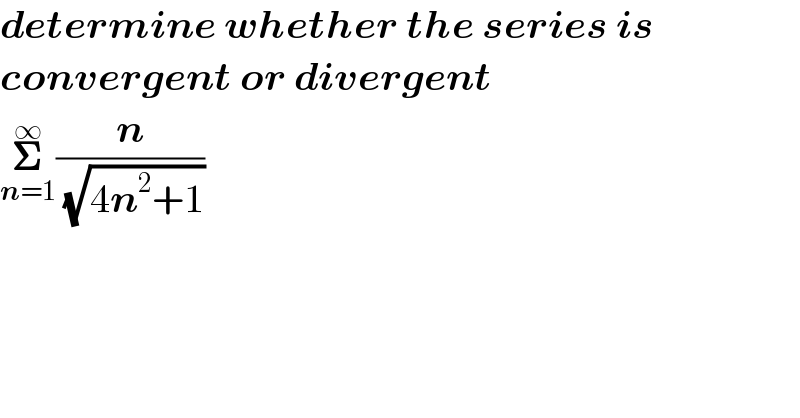
determine whether the series is convergent or divergent 𝚺_(n=1) ^∞ (n/( (√(4n^2 +1))))

$$\boldsymbol{{determine}}\:\boldsymbol{{whether}}\:\boldsymbol{{the}}\:\boldsymbol{{series}}\:\boldsymbol{{is}} \\ $$$$\boldsymbol{{convergent}}\:\boldsymbol{{or}}\:\boldsymbol{{divergent}} \\ $$$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\boldsymbol{\sum}}}\frac{\boldsymbol{{n}}}{\:\sqrt{\mathrm{4}\boldsymbol{{n}}^{\mathrm{2}} +\mathrm{1}}} \\ $$

Answered by witcher3 last updated on 27/Jan/24

(n/( (√(4n^2 +1))))β‰₯(n/( (√(1+4n^2 +4n))))=(n/(2n+1))=((3n)/(3(2n+1)))>((2n+1)/(3(2n+1))) β‡’Ξ£(n/( (√(4n^2 +1))))>Ξ£(1/3) Dv

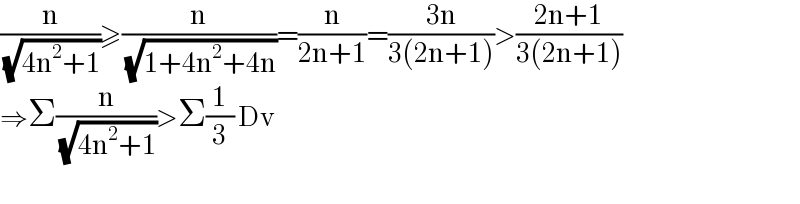
$$\frac{\mathrm{n}}{\:\sqrt{\mathrm{4n}^{\mathrm{2}} +\mathrm{1}}}\geqslant\frac{\mathrm{n}}{\:\sqrt{\mathrm{1}+\mathrm{4n}^{\mathrm{2}} +\mathrm{4n}}}=\frac{\mathrm{n}}{\mathrm{2n}+\mathrm{1}}=\frac{\mathrm{3n}}{\mathrm{3}\left(\mathrm{2n}+\mathrm{1}\right)}>\frac{\mathrm{2n}+\mathrm{1}}{\mathrm{3}\left(\mathrm{2n}+\mathrm{1}\right)} \\ $$$$\Rightarrow\Sigma\frac{\mathrm{n}}{\:\sqrt{\mathrm{4n}^{\mathrm{2}} +\mathrm{1}}}>\Sigma\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{Dv} \\ $$$$ \\ $$

Answered by Mathspace last updated on 30/Jan/24

(n/( (√(4n^2 +1))))=(n/(2n(√(1+(1/(4n^2 ))))))=(1/(2(√(1+(1/(4n^2 )))))) we have (1+x)^Ξ± =1+Ξ±x +((Ξ±(Ξ±βˆ’1))/2)x^2 +o(x^2 )β‡’ (1/( (√(1+x))))=(1+x)^(βˆ’(1/2)) =1βˆ’(x/2)+(1/2)(βˆ’(1/2))(βˆ’(1/2)βˆ’1)x^2 +o(x^2 ) =1βˆ’(x/2)βˆ’(1/4)Γ—((βˆ’3)/2) x^2 +o(x^2 ) =1βˆ’(x/2)+(3/8)x^2 +o(x^2 )so u_n =(1/( 2(√(1+(1/(4n^2 ))))))=(1/2)βˆ’(1/(16n^2 ))+(3/(16))Γ—(1/(16n^4 ))+o((1/n^4 )) est un dev.assymtotique de u_n ona lim u_n =(1/2) β‰ 0 β‡’ Ξ£u_n est divergente.

$$\frac{{n}}{\:\sqrt{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}}}=\frac{{n}}{\mathrm{2}{n}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }}} \\ $$$${we}\:{have}\:\left(\mathrm{1}+{x}\right)^{\alpha} =\mathrm{1}+\alpha{x}\:+\frac{\alpha\left(\alphaβˆ’\mathrm{1}\right)}{\mathrm{2}}{x}^{\mathrm{2}} +{o}\left({x}^{\mathrm{2}} \right)\Rightarrow \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}}}=\left(\mathrm{1}+{x}\right)^{βˆ’\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\mathrm{1}βˆ’\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\left(βˆ’\frac{\mathrm{1}}{\mathrm{2}}\right)\left(βˆ’\frac{\mathrm{1}}{\mathrm{2}}βˆ’\mathrm{1}\right){x}^{\mathrm{2}} +{o}\left({x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{1}βˆ’\frac{{x}}{\mathrm{2}}βˆ’\frac{\mathrm{1}}{\mathrm{4}}Γ—\frac{βˆ’\mathrm{3}}{\mathrm{2}}\:{x}^{\mathrm{2}} +{o}\left({x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{1}βˆ’\frac{{x}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{8}}{x}^{\mathrm{2}} +{o}\left({x}^{\mathrm{2}} \right){so} \\ $$$${u}_{{n}} =\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }}}=\frac{\mathrm{1}}{\mathrm{2}}βˆ’\frac{\mathrm{1}}{\mathrm{16}{n}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{16}}Γ—\frac{\mathrm{1}}{\mathrm{16}{n}^{\mathrm{4}} }+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\right) \\ $$$${est}\:{un}\:{dev}.{assymtotique}\:{de} \\ $$$${u}_{{n}} \:\:\:\:{ona}\:{lim}\:{u}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\:\neq\mathrm{0}\:\Rightarrow \\ $$$$\Sigma{u}_{{n}} \:{est}\:{divergente}. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com