
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 99460 by mathmax by abdo last updated on 21/Jun/20
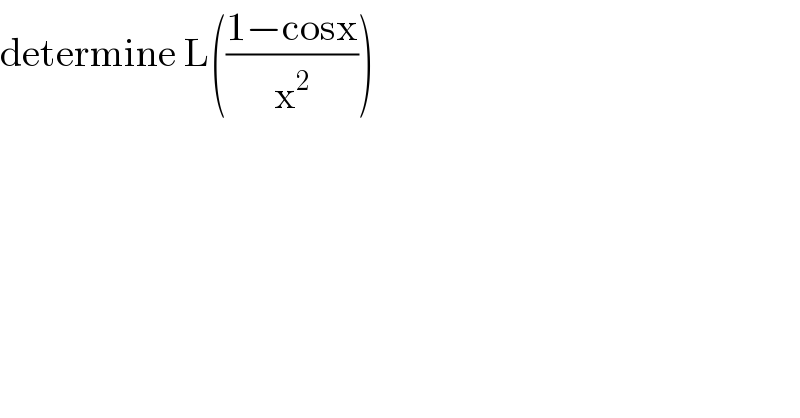
Answered by mathmax by abdo last updated on 23/Jun/20
![L(((1−cosx)/x^2 )) =∫_0 ^∞ ((1−cost)/t^2 )e^(−xt) dt =f(x) ⇒ f^′ (x) =−∫_0 ^∞ (((1−cost)e^(−xt) )/t)dt ⇒f^((2)) (x) =∫_0 ^∞ (1−cost)e^(−xt) dt =∫_0 ^∞ e^(−xt) dt −∫_0 ^∞ e^(−xt) cost dt but ∫_0 ^∞ e^(−xt) dt =[−(1/x)e^(−xt) ]_0 ^∞ =(1/x) and ∫_0 ^∞ e^(−xt) cost dt =Re(∫_0 ^∞ e^(−xt+it) dt) =Re(∫_0 ^∞ e^((−x+i)t) dt) ∫_0 ^∞ e^((−x+i)t) dt =[(1/(−x+i))e^((−x+i)t) ]_0 ^∞ =−(1/(−x+i)) =(1/(x−i)) =((x+i)/(x^2 +1)) ⇒ Re(...) =(x/(x^2 +1)) ⇒f^((2)) (x) =(1/x)−(x/(x^2 +1)) ⇒ f^′ (x) =lnx −(1/2)ln(x^2 +1) +k ⇒ f(x) =∫ ln(x)dx −(1/2)∫ ln(x^2 +1)dx+kx +c we have ∫ ln(x)dx =xln(x)−x ∫ ln(x^2 +1)dx =xln(x^2 +1)−∫ x×((2x)/(1+x^2 ))dx =xln(x^2 +1)−2 ∫ ((x^2 +1−1)/(1+x^2 ))dx =xln(1+x^2 )−2x +2arctanx ⇒ f(x) =xlnx−x−(x/2)ln(1+x^2 )+x −arctanx +kx +c c =lim_(x→0) f(x) =∫_0 ^∞ ((1−cost)/t^2 ) =2 ∫_0 ^∞ ((sin^2 t)/t^2 )dt =2{ [−((sin^2 t)/t)]_0 ^∞ +∫_0 ^∞ ((2sintcost)/t) dt} =2 ∫_0 ^∞ ((sin(2t))/t) dt =_(2t=u) 2∫_0 ^∞ ((sinu)/(u/2))×(du/2) =2∫_0 ^∞ ((sinu)/u)du =π ⇒c =π rest to find k ....be continued....](Q99794.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 99460 by mathmax by abdo last updated on 21/Jun/20 | ||
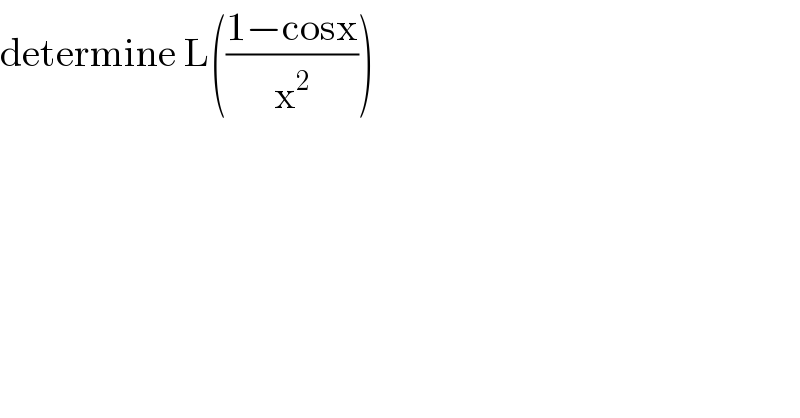 | ||
Answered by mathmax by abdo last updated on 23/Jun/20 | ||
![L(((1−cosx)/x^2 )) =∫_0 ^∞ ((1−cost)/t^2 )e^(−xt) dt =f(x) ⇒ f^′ (x) =−∫_0 ^∞ (((1−cost)e^(−xt) )/t)dt ⇒f^((2)) (x) =∫_0 ^∞ (1−cost)e^(−xt) dt =∫_0 ^∞ e^(−xt) dt −∫_0 ^∞ e^(−xt) cost dt but ∫_0 ^∞ e^(−xt) dt =[−(1/x)e^(−xt) ]_0 ^∞ =(1/x) and ∫_0 ^∞ e^(−xt) cost dt =Re(∫_0 ^∞ e^(−xt+it) dt) =Re(∫_0 ^∞ e^((−x+i)t) dt) ∫_0 ^∞ e^((−x+i)t) dt =[(1/(−x+i))e^((−x+i)t) ]_0 ^∞ =−(1/(−x+i)) =(1/(x−i)) =((x+i)/(x^2 +1)) ⇒ Re(...) =(x/(x^2 +1)) ⇒f^((2)) (x) =(1/x)−(x/(x^2 +1)) ⇒ f^′ (x) =lnx −(1/2)ln(x^2 +1) +k ⇒ f(x) =∫ ln(x)dx −(1/2)∫ ln(x^2 +1)dx+kx +c we have ∫ ln(x)dx =xln(x)−x ∫ ln(x^2 +1)dx =xln(x^2 +1)−∫ x×((2x)/(1+x^2 ))dx =xln(x^2 +1)−2 ∫ ((x^2 +1−1)/(1+x^2 ))dx =xln(1+x^2 )−2x +2arctanx ⇒ f(x) =xlnx−x−(x/2)ln(1+x^2 )+x −arctanx +kx +c c =lim_(x→0) f(x) =∫_0 ^∞ ((1−cost)/t^2 ) =2 ∫_0 ^∞ ((sin^2 t)/t^2 )dt =2{ [−((sin^2 t)/t)]_0 ^∞ +∫_0 ^∞ ((2sintcost)/t) dt} =2 ∫_0 ^∞ ((sin(2t))/t) dt =_(2t=u) 2∫_0 ^∞ ((sinu)/(u/2))×(du/2) =2∫_0 ^∞ ((sinu)/u)du =π ⇒c =π rest to find k ....be continued....](Q99794.png) | ||
| ||