
Question Number 202715 by Rasheed.Sindhi last updated on 01/Jan/24

$$\begin{array}{|c|}{\:\:\underset{\mathrm{is}\:\mathrm{2025}} {\mathrm{Square}\:\mathrm{of}\:\mathrm{mean}\:\mathrm{of}\:\mathrm{two}\:\mathrm{numbers}}\:\:}\\\hline\end{array}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\& \\ $$$$\begin{array}{|c|}{\:\:\underset{\:\mathrm{is}\:\mathrm{2026}} {\mathrm{mean}\:\mathrm{of}\:\mathrm{squares}\:\mathrm{of}\:\mathrm{the}\:\mathrm{numbers}}\:\:}\\\hline\end{array} \\ $$$$\:\:\:\:\: \\ $$$$\begin{array}{|c|}{\mathrm{Find}\:\mathrm{the}\:\mathrm{product}\:\mathrm{of}\:\mathrm{the}\:\mathrm{numbers}.}\\\hline\end{array}\: \\ $$
Answered by JDamian last updated on 01/Jan/24
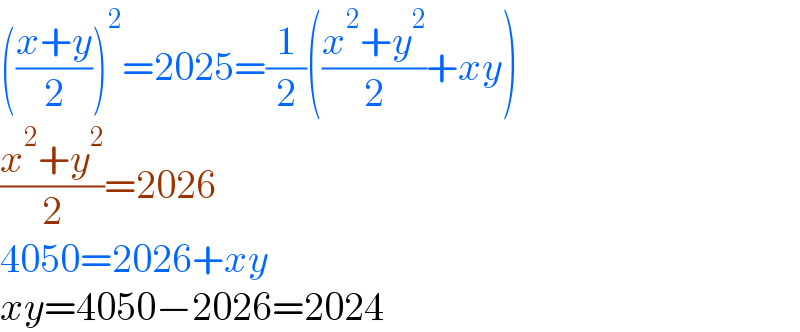
$$\left(\frac{{x}+{y}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{2025}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}+{xy}\right) \\ $$$$\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{2026} \\ $$$$\mathrm{4050}=\mathrm{2026}+{xy} \\ $$$${xy}=\mathrm{4050}−\mathrm{2026}=\mathrm{2024} \\ $$
Commented by Rasheed.Sindhi last updated on 01/Jan/24

$$\mathcal{T}{hanks}\:{sir}! \\ $$$$\mathrm{2024}\checkmark\: \\ $$$$\begin{array}{|c|}{\overset{\mathbb{HAPPY}} {\mathbb{NEW}\:\mathbb{YEAR}!}}\\\hline\end{array} \\ $$
Answered by professorleiciano last updated on 01/Jan/24

$$ \\ $$
