Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 218119 by MrGaster last updated on 30/Mar/25

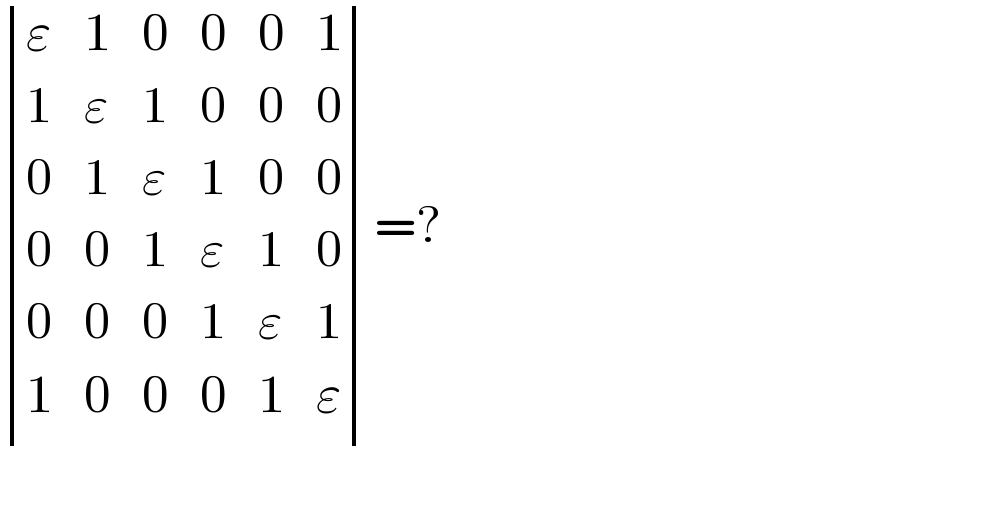
determinant ((ε,1,0,0,0,1),(1,ε,1,0,0,0),(0,1,ε,1,0,0),(0,0,1,ε,1,0),(0,0,0,1,ε,1),(1,0,0,0,1,ε))=?

$$\begin{vmatrix}{\varepsilon}&{\mathrm{1}}&{\mathrm{0}}&{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}\\{\mathrm{1}}&{\varepsilon}&{\mathrm{1}}&{\mathrm{0}}&{\mathrm{0}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{1}}&{\varepsilon}&{\mathrm{1}}&{\mathrm{0}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}&{\varepsilon}&{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}&{\varepsilon}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{0}}&{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}&{\varepsilon}\end{vmatrix}=? \\ $$$$ \\ $$

Answered by SdC355 last updated on 30/Mar/25

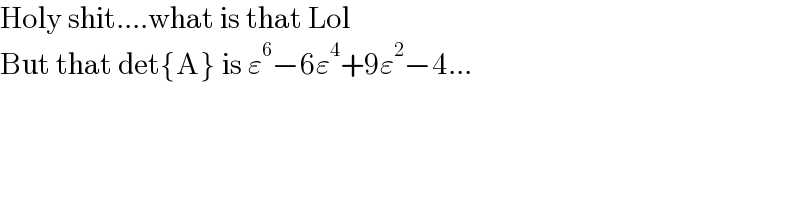
Holy shit....what is that Lol But that det{A} is ε^6 −6ε^4 +9ε^2 −4...

$$\mathrm{Holy}\:\mathrm{shit}....\mathrm{what}\:\mathrm{is}\:\mathrm{that}\:\mathrm{Lol} \\ $$$$\mathrm{But}\:\mathrm{that}\:\mathrm{det}\left\{\mathrm{A}\right\}\:\mathrm{is}\:\varepsilon^{\mathrm{6}} −\mathrm{6}\varepsilon^{\mathrm{4}} +\mathrm{9}\varepsilon^{\mathrm{2}} −\mathrm{4}... \\ $$

Commented by MrGaster last updated on 30/Mar/25

THANK!

$$\mathscr{THANK}! \\ $$

Commented by Ghisom last updated on 30/Mar/25

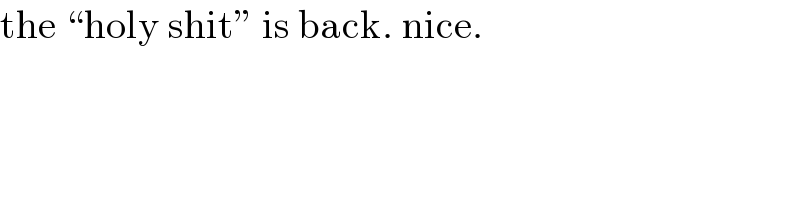
the “holy shit” is back. nice.

$$\mathrm{the}\:``\mathrm{holy}\:\mathrm{shit}''\:\mathrm{is}\:\mathrm{back}.\:\mathrm{nice}. \\ $$

Answered by Wuji last updated on 30/Mar/25

for the 6×6 matrix M(ε)=εI+A for a circulant graph C_n we have eigenvalues of A : 2cos(((2πk)/n)) ⇒k=0,1,...,n−1 for n=6 2,1,−1,−2,−1,1 M(ε)=εI + A ε+2 ,(ε+1)^2 ,(ε−1)^2 ,(ε−2) detM(ε)=(ε+2)(ε+1)^2 (ε−1)^2 (ε−2) detM(ε)=(ε^2 −4)(ε^2 −1)^2

$${for}\:{the}\:\mathrm{6}×\mathrm{6}\:{matrix} \\ $$$${M}\left(\varepsilon\right)=\varepsilon{I}+{A} \\ $$$${for}\:{a}\:{circulant}\:{graph}\:{C}_{{n}} \:{we}\:{have}\:{eigenvalues} \\ $$$${of}\:{A}\:: \\ $$$$\mathrm{2}{cos}\left(\frac{\mathrm{2}\pi{k}}{{n}}\right)\:\:\:\Rightarrow{k}=\mathrm{0},\mathrm{1},...,{n}−\mathrm{1}\: \\ $$$${for}\:{n}=\mathrm{6}\:\: \\ $$$$\mathrm{2},\mathrm{1},−\mathrm{1},−\mathrm{2},−\mathrm{1},\mathrm{1} \\ $$$${M}\left(\varepsilon\right)=\varepsilon{I}\:+\:{A} \\ $$$$\varepsilon+\mathrm{2}\:,\left(\varepsilon+\mathrm{1}\right)^{\mathrm{2}} ,\left(\varepsilon−\mathrm{1}\right)^{\mathrm{2}} ,\left(\varepsilon−\mathrm{2}\right) \\ $$$${detM}\left(\varepsilon\right)=\left(\varepsilon+\mathrm{2}\right)\left(\varepsilon+\mathrm{1}\right)^{\mathrm{2}} \left(\varepsilon−\mathrm{1}\right)^{\mathrm{2}} \left(\varepsilon−\mathrm{2}\right) \\ $$$${detM}\left(\varepsilon\right)=\left(\varepsilon^{\mathrm{2}} −\mathrm{4}\right)\left(\varepsilon^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com