
Question Number 218199 by Mamadi last updated on 01/Apr/25
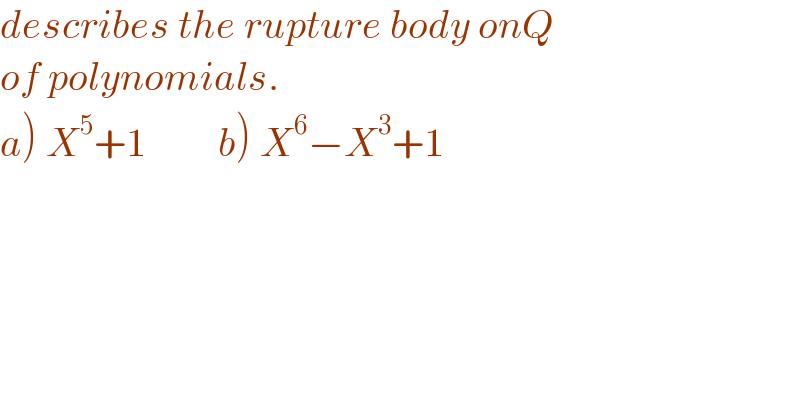
$${describes}\:{the}\:{rupture}\:{body}\:{onQ} \\ $$$${of}\:{polynomials}. \\ $$$$\left.{a}\left.\right)\:{X}^{\mathrm{5}} +\mathrm{1}\:\:\:\:\:\:\:\:\:{b}\right)\:{X}^{\mathrm{6}} −{X}^{\mathrm{3}} +\mathrm{1} \\ $$
Answered by MrGaster last updated on 02/Apr/25
![a:Q(10),Φ_(10) (X)=X^4 −X^3 +X^2 −X+1 ∧[Q(ζ_(10) ):Q]=φ(10)=4 b:Q(ζ_(18) ),Φ_(18) (X)=X^6 −X^3 +1 ∧ [Q(ζ_(18) ):Q]=φ(18)=6](Q218232.png)
$${a}:\mathbb{Q}\left(\mathrm{10}\right),\Phi_{\mathrm{10}} \left({X}\right)={X}^{\mathrm{4}} −{X}^{\mathrm{3}} +{X}^{\mathrm{2}} −{X}+\mathrm{1}\:\wedge\left[\mathbb{Q}\left(\zeta_{\mathrm{10}} \right):\mathbb{Q}\right]=\phi\left(\mathrm{10}\right)=\mathrm{4} \\ $$$${b}:\mathbb{Q}\left(\zeta_{\mathrm{18}} \right),\Phi_{\mathrm{18}} \left({X}\right)={X}^{\mathrm{6}} −{X}^{\mathrm{3}} +\mathrm{1}\:\wedge\:\left[\mathbb{Q}\left(\zeta_{\mathrm{18}} \right):\mathbb{Q}\right]=\phi\left(\mathrm{18}\right)=\mathrm{6} \\ $$
