Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 153565 by talminator2856791 last updated on 08/Sep/21

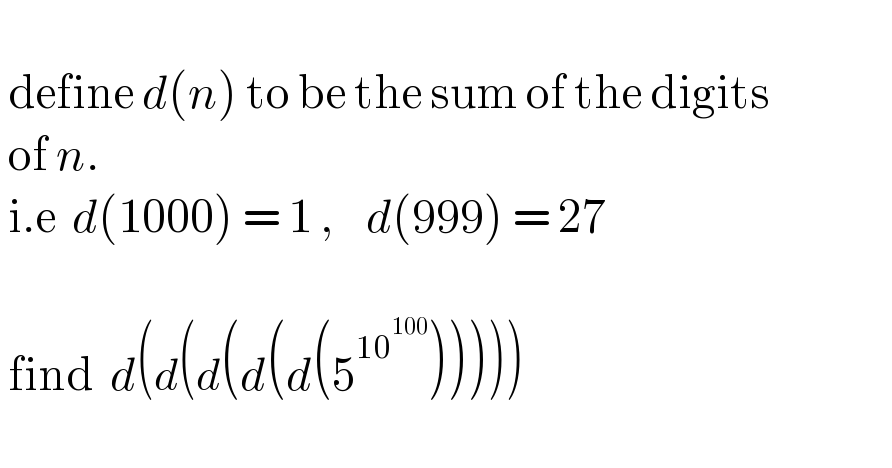
define d(n) to be the sum of the digits of n. i.e d(1000) = 1 , d(999) = 27 find d(d(d(d(d(5^(10^(100) ) )))))

$$\: \\ $$$$\:\mathrm{define}\:{d}\left({n}\right)\:\mathrm{to}\:\mathrm{be}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{digits}\:\: \\ $$$$\:\mathrm{of}\:{n}.\:\:\: \\ $$$$\:\mathrm{i}.\mathrm{e}\:\:{d}\left(\mathrm{1000}\right)\:=\:\mathrm{1}\:,\:\:\:\:{d}\left(\mathrm{999}\right)\:=\:\mathrm{27} \\ $$$$\: \\ $$$$\:\mathrm{find}\:\:{d}\left({d}\left({d}\left({d}\left({d}\left(\mathrm{5}^{\mathrm{10}^{\mathrm{100}} } \right)\right)\right)\right)\right) \\ $$$$\: \\ $$

Commented by Rasheed.Sindhi last updated on 08/Sep/21

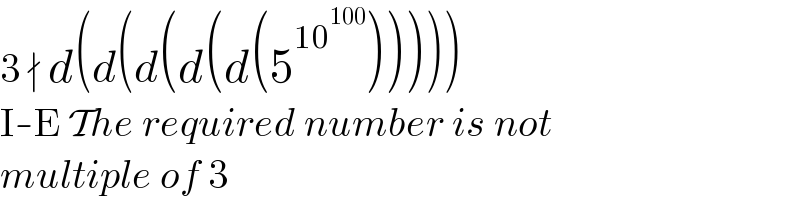
3 ∤ d(d(d(d(d(5^(10^(100) ) ))))) I-E The required number is not multiple of 3

$$\mathrm{3}\:\nmid\:{d}\left({d}\left({d}\left({d}\left({d}\left(\mathrm{5}^{\mathrm{10}^{\mathrm{100}} } \right)\right)\right)\right)\right) \\ $$$$\mathrm{I}-\mathrm{E}\:\mathcal{T}{he}\:{required}\:{number}\:{is}\:{not} \\ $$$${multiple}\:{of}\:\mathrm{3} \\ $$

Commented by talminator2856791 last updated on 08/Sep/21

proof?

$$\:\mathrm{proof}? \\ $$

Commented by Rasheed.Sindhi last updated on 09/Sep/21

If you sufficiently apply d to get answer in one digit you will ultimately get 4. If you want one digit answer I have a solution.

$${If}\:{you}\:{sufficiently}\:{apply}\:{d}\:{to}\:{get} \\ $$$${answer}\:{in}\:{one}\:{digit}\:{you}\:{will}\:{ultimately} \\ $$$${get}\:\mathrm{4}.\:{If}\:{you}\:{want}\:{one}\:{digit}\:{answer} \\ $$$${I}\:{have}\:{a}\:{solution}. \\ $$

Commented by talminator2856791 last updated on 09/Sep/21

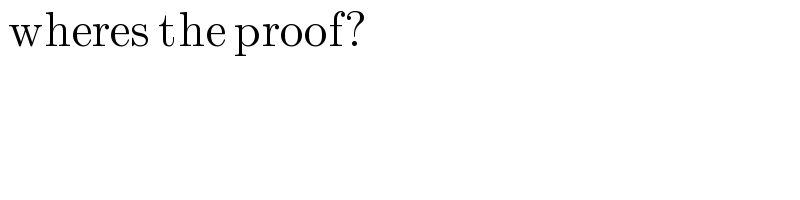
wheres the proof?

$$\:\mathrm{wheres}\:\mathrm{the}\:\mathrm{proof}? \\ $$

Answered by Rasheed.Sindhi last updated on 10/Sep/21

Relation between sum of digits and remainder modulo 9: 5^(10^(100) ) ≡d(d(d(d(d(5^(10^(100) ) )))))(mod 9) We can verify easily that 5^6 ≡1(mod 9) (5^6 )^k ≡1^k (mod 9) 5^(6k) ≡1(mod 9) { ((5^(6k) ≡1(mod 9))),((5^(6k+1) ≡5(mod 9))),((5^(6k+2) ≡7(mod 9))),((5^(6k+3) ≡8(mod 9))),((5^(6k+4) ≡4(mod 9)^★ )),((5^(6k+5) ≡2(mod 9))) :} 5^(10^(100) ) =5^(6k+ ?) { ((10≡4(mod 6))),((10^2 ≡4(mod 6)),((...)),((10^(100) ≡4(mod 6))) :} 5^(10^(100) ) =5^(6k+ 4) d(d(d(d(d(5^(10^(100) ) )))))≡5^(10^(100) ) (mod 9) d(d(d(d(d(5^(10^(100) ) )))))≡5^(6k+4) (mod 9) But we′ve determined before that 5^(6k+4) ≡4(mod 9)^★ ∴d(d(d(d(d(5^(10^(100) ) )))))≡4(mod 9) ∴ Ultimately sum of digits will be 4 if we apply sufficiently the function d over the number 5^(10^(100) ) .

$$ \\ $$$$\mathcal{R}{elation}\:{between}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{digits}\:{and} \\ $$$$\mathrm{remainder}\:\mathrm{modulo}\:\mathrm{9}: \\ $$$$\mathrm{5}^{\mathrm{10}^{\mathrm{100}} } \equiv{d}\left({d}\left({d}\left({d}\left({d}\left(\mathrm{5}^{\mathrm{10}^{\mathrm{100}} } \right)\right)\right)\right)\right)\left({mod}\:\mathrm{9}\right) \\ $$$${We}\:{can}\:{verify}\:{easily}\:{that} \\ $$$$\mathrm{5}^{\mathrm{6}} \equiv\mathrm{1}\left({mod}\:\mathrm{9}\right) \\ $$$$\left(\mathrm{5}^{\mathrm{6}} \right)^{{k}} \equiv\mathrm{1}^{{k}} \left({mod}\:\mathrm{9}\right) \\ $$$$\mathrm{5}^{\mathrm{6}{k}} \equiv\mathrm{1}\left({mod}\:\mathrm{9}\right) \\ $$$$\begin{cases}{\mathrm{5}^{\mathrm{6}{k}} \equiv\mathrm{1}\left({mod}\:\mathrm{9}\right)}\\{\mathrm{5}^{\mathrm{6}{k}+\mathrm{1}} \equiv\mathrm{5}\left({mod}\:\mathrm{9}\right)}\\{\mathrm{5}^{\mathrm{6}{k}+\mathrm{2}} \equiv\mathrm{7}\left({mod}\:\mathrm{9}\right)}\\{\mathrm{5}^{\mathrm{6}{k}+\mathrm{3}} \equiv\mathrm{8}\left({mod}\:\mathrm{9}\right)}\\{\mathrm{5}^{\mathrm{6}{k}+\mathrm{4}} \equiv\mathrm{4}\left({mod}\:\mathrm{9}\right)^{\bigstar} }\\{\mathrm{5}^{\mathrm{6}{k}+\mathrm{5}} \equiv\mathrm{2}\left({mod}\:\mathrm{9}\right)}\end{cases} \\ $$$$\mathrm{5}^{\mathrm{10}^{\mathrm{100}} } =\mathrm{5}^{\mathrm{6}{k}+\:?} \\ $$$$\begin{cases}{\mathrm{10}\equiv\mathrm{4}\left({mod}\:\mathrm{6}\right)}\\{\mathrm{10}^{\mathrm{2}} \equiv\mathrm{4}\left({mod}\:\mathrm{6}\right.}\\{...}\\{\mathrm{10}^{\mathrm{100}} \equiv\mathrm{4}\left({mod}\:\mathrm{6}\right)}\end{cases} \\ $$$$\mathrm{5}^{\mathrm{10}^{\mathrm{100}} } =\mathrm{5}^{\mathrm{6}{k}+\:\mathrm{4}} \\ $$$${d}\left({d}\left({d}\left({d}\left({d}\left(\mathrm{5}^{\mathrm{10}^{\mathrm{100}} } \right)\right)\right)\right)\right)\equiv\mathrm{5}^{\mathrm{10}^{\mathrm{100}} } \left({mod}\:\mathrm{9}\right) \\ $$$${d}\left({d}\left({d}\left({d}\left({d}\left(\mathrm{5}^{\mathrm{10}^{\mathrm{100}} } \right)\right)\right)\right)\right)\equiv\mathrm{5}^{\mathrm{6}{k}+\mathrm{4}} \left({mod}\:\mathrm{9}\right) \\ $$$${But}\:{we}'{ve}\:{determined}\:{before}\:{that} \\ $$$$\:\:\:\:\:\:\:\mathrm{5}^{\mathrm{6}{k}+\mathrm{4}} \equiv\mathrm{4}\left({mod}\:\mathrm{9}\right)^{\bigstar} \\ $$$$\therefore{d}\left({d}\left({d}\left({d}\left({d}\left(\mathrm{5}^{\mathrm{10}^{\mathrm{100}} } \right)\right)\right)\right)\right)\equiv\mathrm{4}\left({mod}\:\mathrm{9}\right) \\ $$$$\therefore\:{Ultimately}\:{sum}\:{of}\:{digits}\:{will}\:{be} \\ $$$$\mathrm{4}\:{if}\:{we}\:{apply}\:{sufficiently}\:{the}\:{function} \\ $$$$\boldsymbol{{d}}\:{over}\:{the}\:{number}\:\:\mathrm{5}^{\mathrm{10}^{\mathrm{100}} } \:. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com