
Previous in Relation and Functions Next in Relation and Functions
Question Number 67672 by Abdo msup. last updated on 30/Aug/19
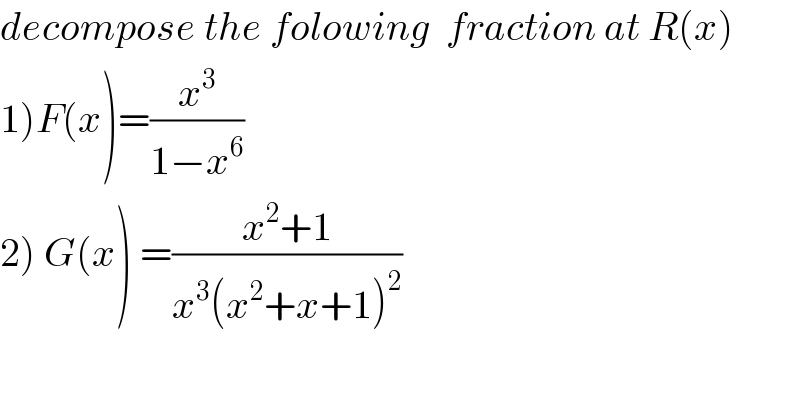
$${decompose}\:{the}\:{folowing}\:\:{fraction}\:{at}\:{R}\left({x}\right) \\ $$$$\left.\mathrm{1}\right){F}\left({x}\right)=\frac{{x}^{\mathrm{3}} }{\mathrm{1}−{x}^{\mathrm{6}} } \\ $$$$\left.\mathrm{2}\right)\:{G}\left({x}\right)\:=\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{3}} \left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by Abdo msup. last updated on 30/Aug/19

$$\left.\mathrm{1}\right){F}\left({x}\right)\:=−\frac{{x}^{\mathrm{3}} }{\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} −\mathrm{1}}\:=−\frac{{x}^{\mathrm{3}} }{\left({x}^{\mathrm{3}} −\mathrm{1}\right)\left({x}^{\mathrm{3}} \:+\mathrm{1}\right)} \\ $$$$=\frac{−{x}^{\mathrm{3}} }{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)} \\ $$$$=\frac{{a}}{{x}−\mathrm{1}}\:+\frac{{b}}{{x}+\mathrm{1}}\:+\frac{{cx}\:+{d}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:+\frac{{ex}\:+{f}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}} \\ $$$${a}\:={lim}_{{x}\rightarrow\mathrm{1}} \left({x}−\mathrm{1}\right){F}\left({x}\right)\:=−\frac{\mathrm{1}}{\mathrm{3}.\mathrm{2}.\mathrm{1}}\:=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${b}\:={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)=\frac{\mathrm{1}}{\left(−\mathrm{2}\right).\mathrm{3}}=−\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{−\mathrm{1}}{\mathrm{6}\left({x}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{6}\left({x}+\mathrm{1}\right)}\:+\frac{{cx}+{d}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:+\frac{{ex}\:+{f}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$${F}\left(−{x}\right)\:=−{F}\left({x}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{6}\left({x}+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{6}\left({x}−\mathrm{1}\right)}\:+\frac{−{cx}+{d}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}\:+\frac{−{ex}\:+{f}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}\left({x}−\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{6}\left({x}+\mathrm{1}\right)}\:+\frac{−{cx}\:−{d}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:+\frac{−{ex}−{f}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}\:\Rightarrow \\ $$$$\Rightarrow\:{f}=−{d}... \\ $$$$ \\ $$$$ \\ $$
Commented by Abdo msup. last updated on 30/Aug/19

$$\Rightarrow\:{F}\left({x}\right)\:=−\frac{\mathrm{1}}{\mathrm{6}\left({x}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{6}\left({x}+\mathrm{1}\right)}\:+\frac{{cx}\:+{d}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:+\frac{{ex}−{d}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)\:=\mathrm{0}\:=−\frac{\mathrm{1}}{\mathrm{3}}\:+{c}+{e}\:\Rightarrow{e}\:=\frac{\mathrm{1}}{\mathrm{3}}−{c}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=−\frac{\mathrm{1}}{\mathrm{6}\left({x}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{6}\left({x}+\mathrm{1}\right)}\:+\frac{{cx}+{d}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:+\frac{\left(\frac{\mathrm{1}}{\mathrm{3}}−{c}\right){x}−{d}}{{x}^{\mathrm{2}} \:−{x}\:+\mathrm{1}} \\ $$$${to}\:{detrmine}\:{c}\:{and}\:{d}\:\:{we}?{can}\:{calculate}\:{F}\left(\mathrm{2}\right)\:{and} \\ $$$${F}\left(−\mathrm{2}\right)...{be}?{vontinued}... \\ $$
