
Previous in Differential Equation Next in Differential Equation
Question Number 175406 by princeDera last updated on 29/Aug/22
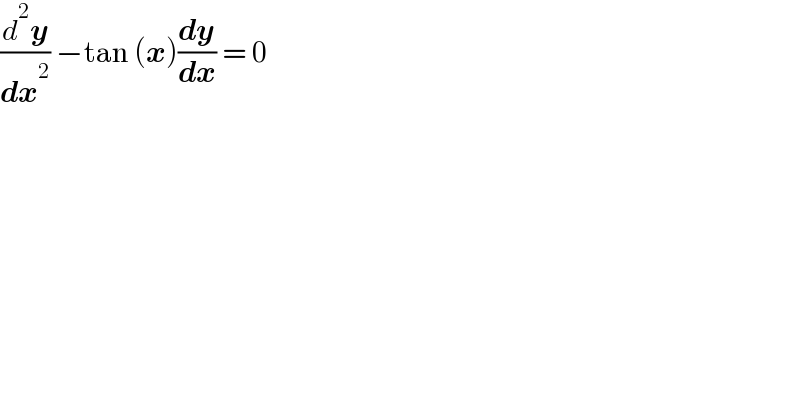
$$\frac{{d}^{\mathrm{2}} \boldsymbol{{y}}}{\boldsymbol{{dx}}^{\mathrm{2}} }\:−\mathrm{tan}\:\left(\boldsymbol{{x}}\right)\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}\:=\:\mathrm{0} \\ $$
Answered by Ar Brandon last updated on 29/Aug/22
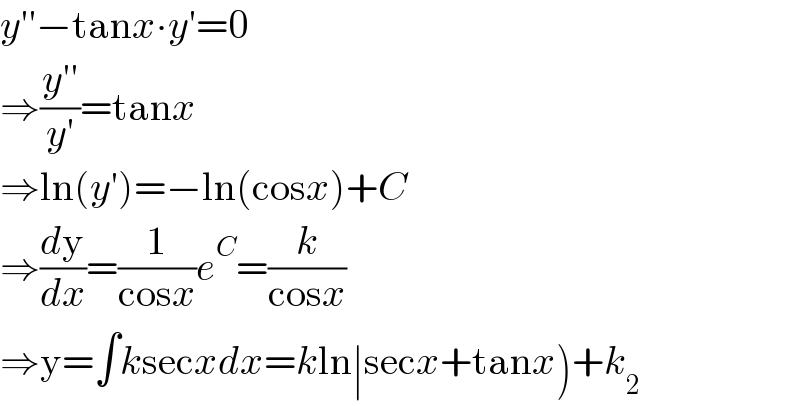
$${y}''−\mathrm{tan}{x}\centerdot{y}'=\mathrm{0} \\ $$$$\Rightarrow\frac{{y}''}{{y}'}=\mathrm{tan}{x} \\ $$$$\Rightarrow\mathrm{ln}\left({y}'\right)=−\mathrm{ln}\left(\mathrm{cos}{x}\right)+{C} \\ $$$$\Rightarrow\frac{{d}\mathrm{y}}{{dx}}=\frac{\mathrm{1}}{\mathrm{cos}{x}}{e}^{{C}} =\frac{{k}}{\mathrm{cos}{x}} \\ $$$$\left.\Rightarrow\mathrm{y}=\int{k}\mathrm{sec}{xdx}={k}\mathrm{ln}\mid\mathrm{sec}{x}+\mathrm{tan}{x}\right)+{k}_{\mathrm{2}} \\ $$
