
Previous in Differential Equation Next in Differential Equation
Question Number 73495 by ajfour last updated on 13/Nov/19
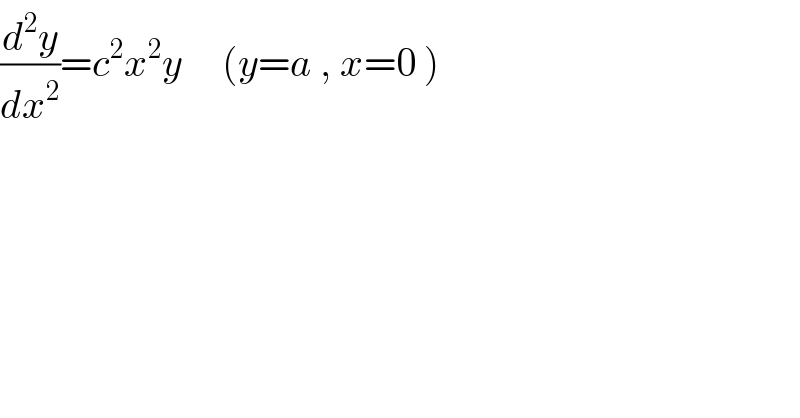
$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }={c}^{\mathrm{2}} {x}^{\mathrm{2}} {y}\:\:\:\:\:\left({y}={a}\:,\:{x}=\mathrm{0}\:\right) \\ $$
Answered by mind is power last updated on 13/Nov/19
![t=x^2 (dy/dx)=(dy/dt).(dt/dx)=2x(dy/dt) (d^2 y/dx^2 )=2(dy/dt)+2x.(d^2 y/dt^2 ).(dt/dx)=2(dy/dt)+4x^2 (d^2 y/dt^2 ) ⇔4x^2 (d^2 y/dt^2 )+2(dy/dt)=c^2 x^2 y ⇔4t(d^2 y/dt^2 )+2(dy/dt)−c^2 ty(t)=0 ⇔t^2 (d^2 y/dt^2 )+(1/2)t(dy/dt)−(c^2 /4)t^2 y(t)=0 Bessel generalise Equation is x^2 (d^2 y/dx^2 )+(2p+1)x(dy/dx)+(a^2 x^(2r) +β^2 )y=0 solution is y=x^(−p) [C_1 J_(q/r ) (((ax^r )/r))+C_2 Y_(q/r) ((α/r)x^r )] q=(√(p^2 −β^2 )) in our case r=1 a=(((ci)/2)) p=−(1/4) q=(√((1/(16))−0))=(1/4) y=t^(1/4) [C_1 J_(1/4) (((ci)/2)t)+C_2 Y_(1/4) (((cit)/2))] J first bassel function,Y 2nd espace of bassel equation y(x)=Y(t)∣_(t=(√x))](Q73506.png)
$${t}={x}^{\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{dt}}.\frac{{dt}}{{dx}}=\mathrm{2}{x}\frac{{dy}}{{dt}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\mathrm{2}\frac{{dy}}{{dt}}+\mathrm{2}{x}.\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }.\frac{{dt}}{{dx}}=\mathrm{2}\frac{{dy}}{{dt}}+\mathrm{4}{x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} } \\ $$$$\Leftrightarrow\mathrm{4}{x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }+\mathrm{2}\frac{{dy}}{{dt}}={c}^{\mathrm{2}} {x}^{\mathrm{2}} {y} \\ $$$$\Leftrightarrow\mathrm{4}{t}\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }+\mathrm{2}\frac{{dy}}{{dt}}−{c}^{\mathrm{2}} {ty}\left({t}\right)=\mathrm{0} \\ $$$$\Leftrightarrow{t}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}{t}\frac{{dy}}{{dt}}−\frac{{c}^{\mathrm{2}} }{\mathrm{4}}{t}^{\mathrm{2}} {y}\left({t}\right)=\mathrm{0} \\ $$$${Bessel}\:{generalise}\:{Equation} \\ $$$${is}\:{x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\left(\mathrm{2}{p}+\mathrm{1}\right){x}\frac{{dy}}{{dx}}+\left({a}^{\mathrm{2}} {x}^{\mathrm{2}{r}} +\beta^{\mathrm{2}} \right){y}=\mathrm{0} \\ $$$${solution}\:{is}\:{y}={x}^{−{p}} \left[{C}_{\mathrm{1}} {J}_{{q}/{r}\:} \left(\frac{{ax}^{{r}} }{{r}}\right)+{C}_{\mathrm{2}} {Y}_{{q}/{r}} \left(\frac{\alpha}{{r}}{x}^{{r}} \right)\right] \\ $$$${q}=\sqrt{{p}^{\mathrm{2}} −\beta^{\mathrm{2}} } \\ $$$${in}\:{our}\:{case}\:{r}=\mathrm{1} \\ $$$${a}=\left(\frac{{ci}}{\mathrm{2}}\right) \\ $$$${p}=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${q}=\sqrt{\frac{\mathrm{1}}{\mathrm{16}}−\mathrm{0}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${y}={t}^{\frac{\mathrm{1}}{\mathrm{4}}} \left[{C}_{\mathrm{1}} {J}_{\frac{\mathrm{1}}{\mathrm{4}}} \left(\frac{{ci}}{\mathrm{2}}{t}\right)+{C}_{\mathrm{2}} {Y}_{\frac{\mathrm{1}}{\mathrm{4}}} \left(\frac{{cit}}{\mathrm{2}}\right)\right] \\ $$$${J}\:\:{first}\:{bassel}\:{function},{Y}\:\:\mathrm{2}{nd}\:{espace}\:{of}\:{bassel}\:{equation} \\ $$$${y}\left({x}\right)={Y}\left({t}\right)\mid_{{t}=\sqrt{{x}}} \\ $$
Commented by ajfour last updated on 13/Nov/19

$${Thanks}\:'{Powerful}\:{Mind}'\:,\:{i}'{ll} \\ $$$${look}\:{into}\:'{Erwin}\:{Kreyszig}' \\ $$$$\left({higher}\:{engg}.\:{maths}\:{book}\right)\:{and} \\ $$$${try}\:{to}\:{understand}\:{your}\:{sol}^{{n}} .. \\ $$
Commented by mind is power last updated on 13/Nov/19

$${y}'{re}\:{Welcom}\:\:\:{i}\:{had}\:{a}\:{pdf}\:{of}\:\:{differential}\:{equation} \\ $$$${if}\:{i}\:{find}\:{it}\:{i}\:{tell}\:{you}\:{the}\:{Names} \\ $$
