
Question Number 47035 by 23kpratik last updated on 04/Nov/18

$$\left({d}^{\mathrm{2}} +{a}^{\mathrm{2}} \right){y}={tan}\:{ax}\:{by}\:{the}\:{method}\:{of}\:{variation}\:{of}\:{parameters} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 04/Nov/18
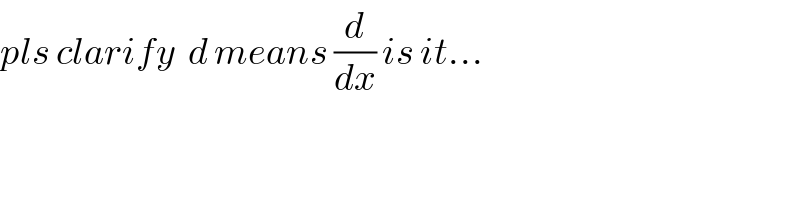
$${pls}\:{clarify}\:\:{d}\:{means}\:\frac{{d}}{{dx}}\:{is}\:{it}... \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Nov/18

$${y}=\frac{\mathrm{1}}{{D}^{\mathrm{2}} +{a}^{\mathrm{2}} }{tanax} \\ $$$$=\frac{\mathrm{1}}{{D}^{\mathrm{2}} +{a}^{\mathrm{2}} }×\frac{\mathrm{2}{isinax}}{{i}×\mathrm{2}{cosax}} \\ $$$$=\frac{\mathrm{1}}{{D}^{\mathrm{2}} +{a}^{\mathrm{2}} }×\frac{{e}^{{iax}} −{e}^{−{iax}} }{{i}×\left({e}^{{iax}} +{e}^{−{iax}} \right)} \\ $$$${e}^{{iax}} ={cosax}+{isinax} \\ $$$${e}^{−{iax}} ={cosax}−{isinax} \\ $$$${y}=\frac{\mathrm{1}}{\left({D}+{ia}\right)\left({D}−{ia}\right)}×\frac{\mathrm{1}}{{i}}×\frac{{e}^{{i}\mathrm{2}{ax}} −\mathrm{1}}{{e}^{{i}\mathrm{2}{ax}} +\mathrm{1}} \\ $$$$={wait}... \\ $$
