Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 76469 by kaivan.ahmadi last updated on 27/Dec/19

∫cothx dx

$$\int{cothx}\:{dx} \\ $$

Commented by mathmax by abdo last updated on 27/Dec/19

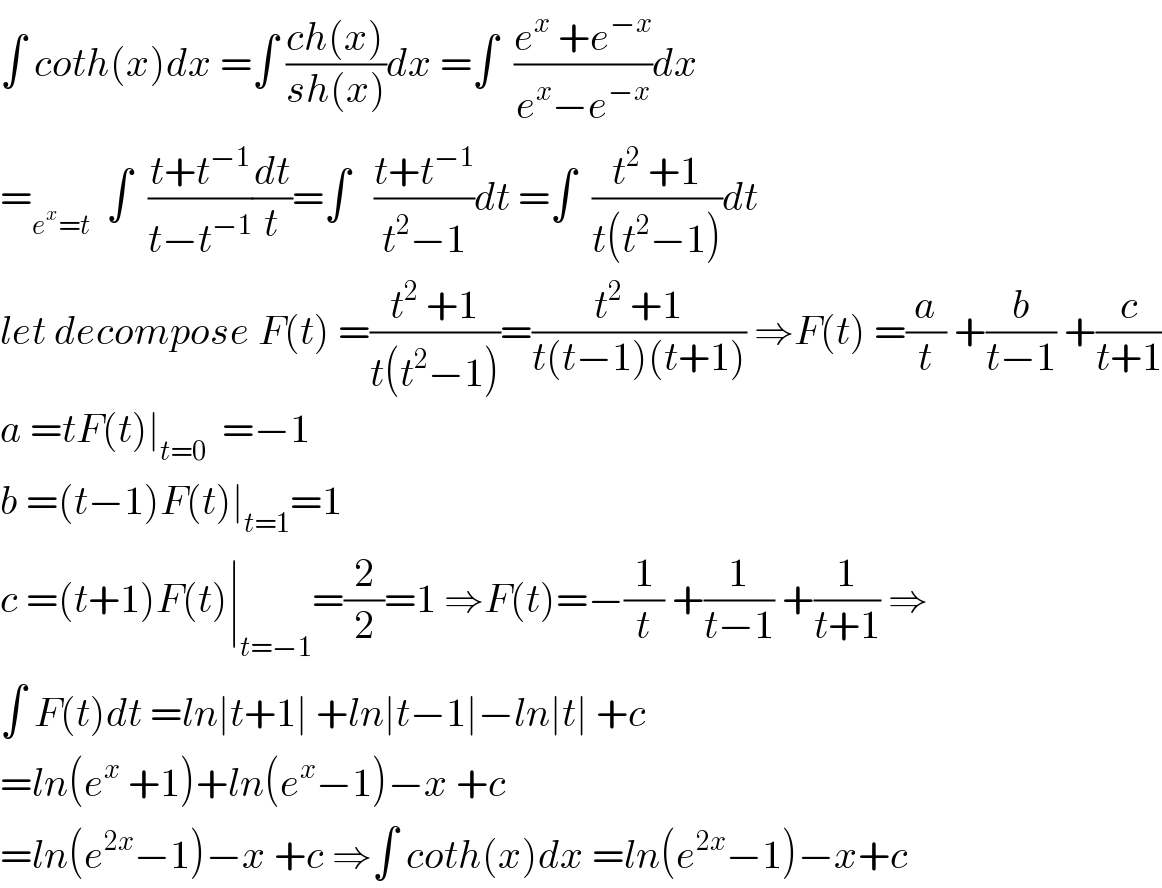
∫ coth(x)dx =∫ ((ch(x))/(sh(x)))dx =∫ ((e^x +e^(−x) )/(e^x −e^(−x) ))dx =_(e^x =t) ∫ ((t+t^(−1) )/(t−t^(−1) ))(dt/t)=∫ ((t+t^(−1) )/(t^2 −1))dt =∫ ((t^2 +1)/(t(t^2 −1)))dt let decompose F(t) =((t^2 +1)/(t(t^2 −1)))=((t^2 +1)/(t(t−1)(t+1))) ⇒F(t) =(a/t) +(b/(t−1)) +(c/(t+1)) a =tF(t)∣_(t=0) =−1 b =(t−1)F(t)∣_(t=1) =1 c =(t+1)F(t)∣_(t=−1) =(2/2)=1 ⇒F(t)=−(1/t) +(1/(t−1)) +(1/(t+1)) ⇒ ∫ F(t)dt =ln∣t+1∣ +ln∣t−1∣−ln∣t∣ +c =ln(e^x +1)+ln(e^x −1)−x +c =ln(e^(2x) −1)−x +c ⇒∫ coth(x)dx =ln(e^(2x) −1)−x+c

$$\int\:{coth}\left({x}\right){dx}\:=\int\:\frac{{ch}\left({x}\right)}{{sh}\left({x}\right)}{dx}\:=\int\:\:\frac{{e}^{{x}} \:+{e}^{−{x}} }{{e}^{{x}} −{e}^{−{x}} }{dx} \\ $$$$=_{{e}^{{x}} ={t}} \:\:\int\:\:\frac{{t}+{t}^{−\mathrm{1}} }{{t}−{t}^{−\mathrm{1}} }\frac{{dt}}{{t}}=\int\:\:\:\frac{{t}+{t}^{−\mathrm{1}} }{{t}^{\mathrm{2}} −\mathrm{1}}{dt}\:=\int\:\:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{dt} \\ $$$${let}\:{decompose}\:{F}\left({t}\right)\:=\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}=\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)}\:\Rightarrow{F}\left({t}\right)\:=\frac{{a}}{{t}}\:+\frac{{b}}{{t}−\mathrm{1}}\:+\frac{{c}}{{t}+\mathrm{1}} \\ $$$${a}\:={tF}\left({t}\right)\mid_{{t}=\mathrm{0}} \:\:=−\mathrm{1} \\ $$$${b}\:=\left({t}−\mathrm{1}\right){F}\left({t}\right)\mid_{{t}=\mathrm{1}} =\mathrm{1} \\ $$$${c}\:=\left({t}+\mathrm{1}\right){F}\left({t}\right)\mid_{{t}=−\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{2}}=\mathrm{1}\:\Rightarrow{F}\left({t}\right)=−\frac{\mathrm{1}}{{t}}\:+\frac{\mathrm{1}}{{t}−\mathrm{1}}\:+\frac{\mathrm{1}}{{t}+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({t}\right){dt}\:={ln}\mid{t}+\mathrm{1}\mid\:+{ln}\mid{t}−\mathrm{1}\mid−{ln}\mid{t}\mid\:+{c} \\ $$$$={ln}\left({e}^{{x}} \:+\mathrm{1}\right)+{ln}\left({e}^{{x}} −\mathrm{1}\right)−{x}\:+{c} \\ $$$$={ln}\left({e}^{\mathrm{2}{x}} −\mathrm{1}\right)−{x}\:+{c}\:\Rightarrow\int\:{coth}\left({x}\right){dx}\:={ln}\left({e}^{\mathrm{2}{x}} −\mathrm{1}\right)−{x}+{c} \\ $$

Commented by mathmax by abdo last updated on 27/Dec/19

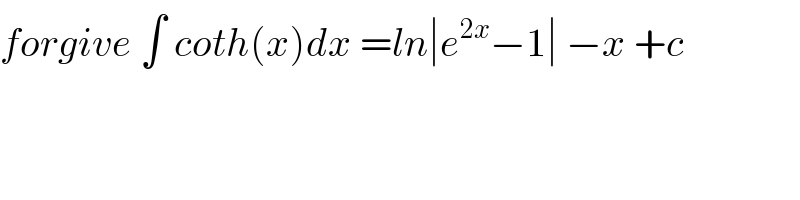
forgive ∫ coth(x)dx =ln∣e^(2x) −1∣ −x +c

$${forgive}\:\int\:{coth}\left({x}\right){dx}\:={ln}\mid{e}^{\mathrm{2}{x}} −\mathrm{1}\mid\:−{x}\:+{c} \\ $$

Commented by kaivan.ahmadi last updated on 29/Dec/19

thank sir

$${thank}\:{sir} \\ $$

Answered by Rio Michael last updated on 27/Dec/19

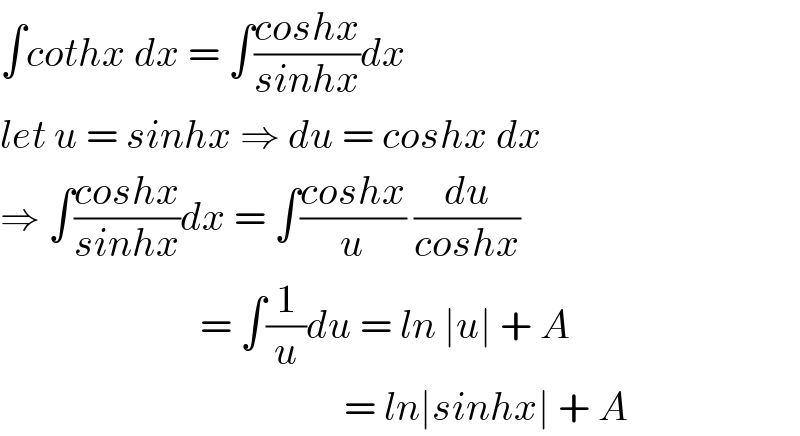
∫cothx dx = ∫((coshx)/(sinhx))dx let u = sinhx ⇒ du = coshx dx ⇒ ∫((coshx)/(sinhx))dx = ∫((coshx)/u) (du/(coshx)) = ∫(1/u)du = ln ∣u∣ + A = ln∣sinhx∣ + A

$$\int{cothx}\:{dx}\:=\:\int\frac{{coshx}}{{sinhx}}{dx} \\ $$$${let}\:{u}\:=\:{sinhx}\:\Rightarrow\:{du}\:=\:{coshx}\:{dx} \\ $$$$\Rightarrow\:\int\frac{{coshx}}{{sinhx}}{dx}\:=\:\int\frac{{coshx}}{{u}}\:\frac{{du}}{{coshx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\int\frac{\mathrm{1}}{{u}}{du}\:=\:{ln}\:\mid{u}\mid\:+\:{A} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{ln}\mid{sinhx}\mid\:+\:{A} \\ $$

Commented by kaivan.ahmadi last updated on 29/Dec/19

thank u

$${thank}\:{u} \\ $$

Answered by Henri Boucatchou last updated on 28/Dec/19

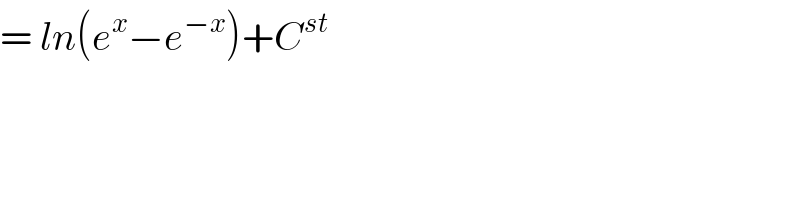
= ln(e^x −e^(−x) )+C^(st)

$$=\:{ln}\left({e}^{{x}} −{e}^{−{x}} \right)+{C}^{{st}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com