
Question Number 89047 by jagoll last updated on 15/Apr/20

$$\mathrm{cos}\:{x}+\mathrm{sin}\:{x}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{5sin}\:{x}\:=\:? \\ $$
Commented by john santu last updated on 15/Apr/20
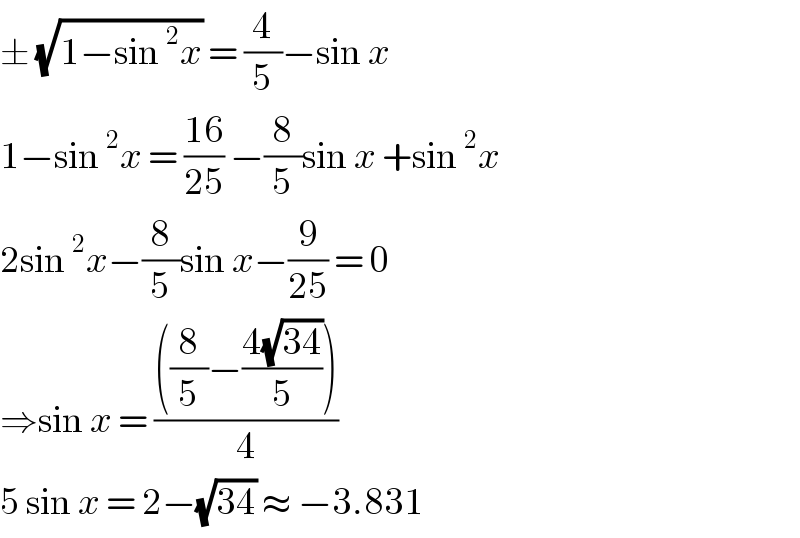
$$\pm\:\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}}\:=\:\frac{\mathrm{4}}{\mathrm{5}}−\mathrm{sin}\:{x} \\ $$$$\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}\:=\:\frac{\mathrm{16}}{\mathrm{25}}\:−\frac{\mathrm{8}}{\mathrm{5}}\mathrm{sin}\:{x}\:+\mathrm{sin}\:^{\mathrm{2}} {x} \\ $$$$\mathrm{2sin}\:^{\mathrm{2}} {x}−\frac{\mathrm{8}}{\mathrm{5}}\mathrm{sin}\:{x}−\frac{\mathrm{9}}{\mathrm{25}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:{x}\:=\:\frac{\left(\frac{\mathrm{8}}{\mathrm{5}}−\frac{\mathrm{4}\sqrt{\mathrm{34}}}{\mathrm{5}}\right)}{\mathrm{4}} \\ $$$$\mathrm{5}\:\mathrm{sin}\:{x}\:=\:\mathrm{2}−\sqrt{\mathrm{34}}\:\approx\:−\mathrm{3}.\mathrm{831} \\ $$
Answered by MJS last updated on 15/Apr/20
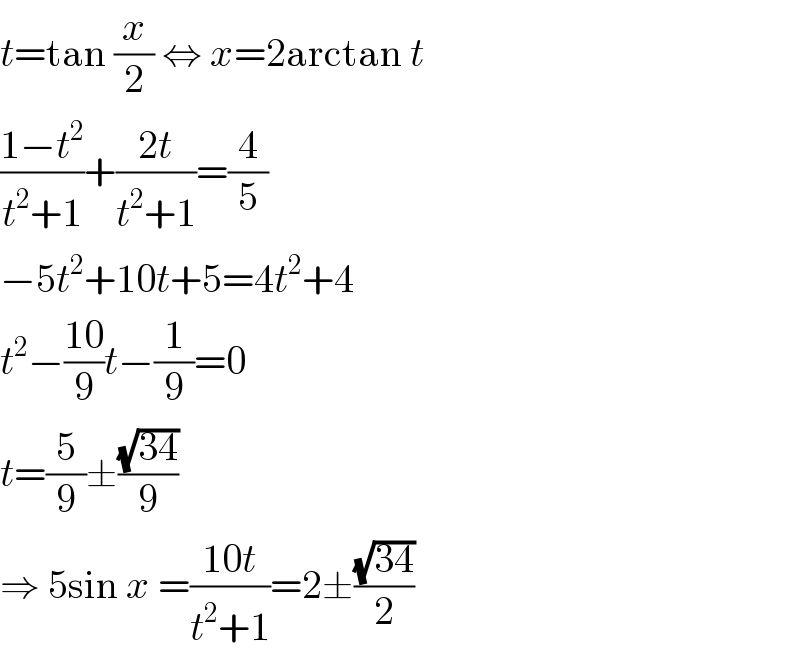
$${t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\Leftrightarrow\:{x}=\mathrm{2arctan}\:{t} \\ $$$$\frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$−\mathrm{5}{t}^{\mathrm{2}} +\mathrm{10}{t}+\mathrm{5}=\mathrm{4}{t}^{\mathrm{2}} +\mathrm{4} \\ $$$${t}^{\mathrm{2}} −\frac{\mathrm{10}}{\mathrm{9}}{t}−\frac{\mathrm{1}}{\mathrm{9}}=\mathrm{0} \\ $$$${t}=\frac{\mathrm{5}}{\mathrm{9}}\pm\frac{\sqrt{\mathrm{34}}}{\mathrm{9}} \\ $$$$\Rightarrow\:\mathrm{5sin}\:{x}\:=\frac{\mathrm{10}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{2}\pm\frac{\sqrt{\mathrm{34}}}{\mathrm{2}} \\ $$
Commented by john santu last updated on 15/Apr/20
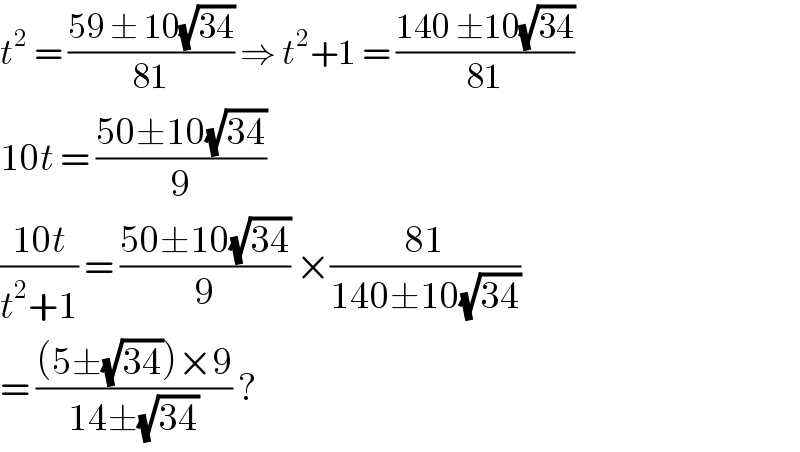
$${t}^{\mathrm{2}} \:=\:\frac{\mathrm{59}\:\pm\:\mathrm{10}\sqrt{\mathrm{34}}}{\mathrm{81}}\:\Rightarrow\:{t}^{\mathrm{2}} +\mathrm{1}\:=\:\frac{\mathrm{140}\:\pm\mathrm{10}\sqrt{\mathrm{34}}}{\mathrm{81}} \\ $$$$\mathrm{10}{t}\:=\:\frac{\mathrm{50}\pm\mathrm{10}\sqrt{\mathrm{34}}}{\mathrm{9}} \\ $$$$\frac{\mathrm{10}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\:=\:\frac{\mathrm{50}\pm\mathrm{10}\sqrt{\mathrm{34}}}{\mathrm{9}}\:×\frac{\mathrm{81}}{\mathrm{140}\pm\mathrm{10}\sqrt{\mathrm{34}}} \\ $$$$=\:\frac{\left(\mathrm{5}\pm\sqrt{\mathrm{34}}\right)×\mathrm{9}}{\mathrm{14}\pm\sqrt{\mathrm{34}}}\:?\: \\ $$
Commented by MJS last updated on 15/Apr/20
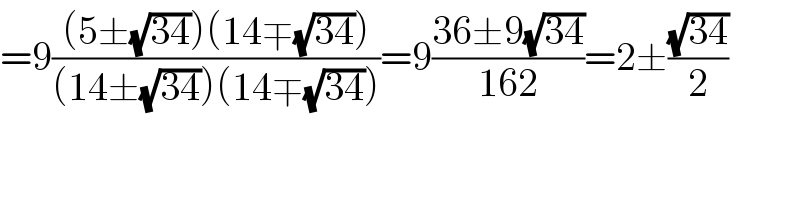
$$=\mathrm{9}\frac{\left(\mathrm{5}\pm\sqrt{\mathrm{34}}\right)\left(\mathrm{14}\mp\sqrt{\mathrm{34}}\right)}{\left(\mathrm{14}\pm\sqrt{\mathrm{34}}\right)\left(\mathrm{14}\mp\sqrt{\mathrm{34}}\right)}=\mathrm{9}\frac{\mathrm{36}\pm\mathrm{9}\sqrt{\mathrm{34}}}{\mathrm{162}}=\mathrm{2}\pm\frac{\sqrt{\mathrm{34}}}{\mathrm{2}} \\ $$
Commented by jagoll last updated on 15/Apr/20
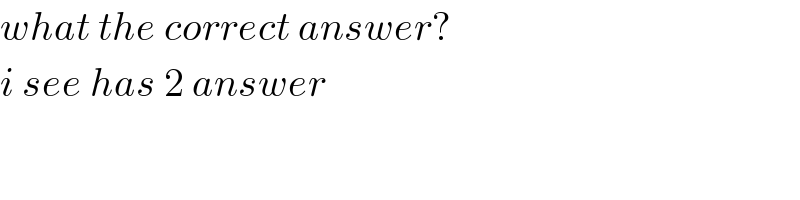
$${what}\:{the}\:{correct}\:{answer}? \\ $$$${i}\:{see}\:{has}\:\mathrm{2}\:{answer}\: \\ $$
Commented by MJS last updated on 15/Apr/20

$$\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}\:=\frac{\mathrm{4}}{\mathrm{5}}\:\mathrm{has}\:\mathrm{2}\:\mathrm{solutions}\:\mathrm{in}\:\left[\mathrm{0};\:\mathrm{2}\pi\left[\right.\right. \\ $$$$\Rightarrow\:\mathrm{2}\:\mathrm{correct}\:\mathrm{answers} \\ $$
Commented by jagoll last updated on 15/Apr/20
$${o}.\:{thanks}\:{very}\:{much}\:{sir}.\: \\ $$
