
Question Number 87069 by jagoll last updated on 02/Apr/20
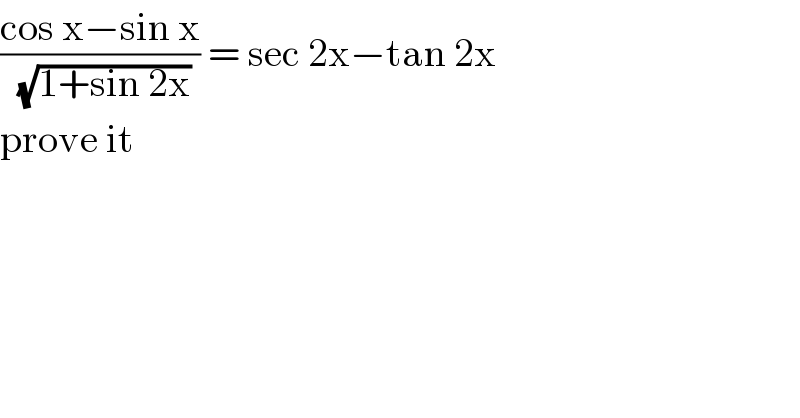
$$\frac{\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{2x}}}\:=\:\mathrm{sec}\:\mathrm{2x}−\mathrm{tan}\:\mathrm{2x} \\ $$$$\mathrm{prove}\:\mathrm{it}\: \\ $$
Commented by jagoll last updated on 02/Apr/20
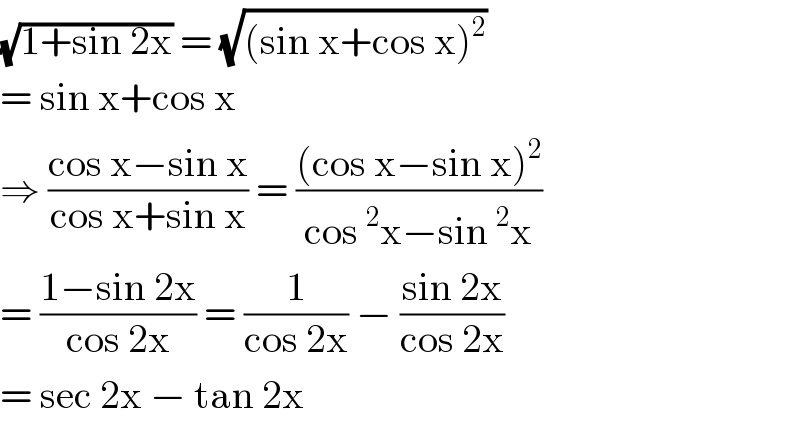
$$\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{2x}}\:=\:\sqrt{\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$=\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\: \\ $$$$\Rightarrow\:\frac{\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}}\:=\:\frac{\left(\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{2}} }{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}} \\ $$$$=\:\frac{\mathrm{1}−\mathrm{sin}\:\mathrm{2x}}{\mathrm{cos}\:\mathrm{2x}}\:=\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{2x}}\:−\:\frac{\mathrm{sin}\:\mathrm{2x}}{\mathrm{cos}\:\mathrm{2x}} \\ $$$$=\:\mathrm{sec}\:\mathrm{2x}\:−\:\mathrm{tan}\:\mathrm{2x} \\ $$
