Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 91825 by john santu last updated on 03/May/20

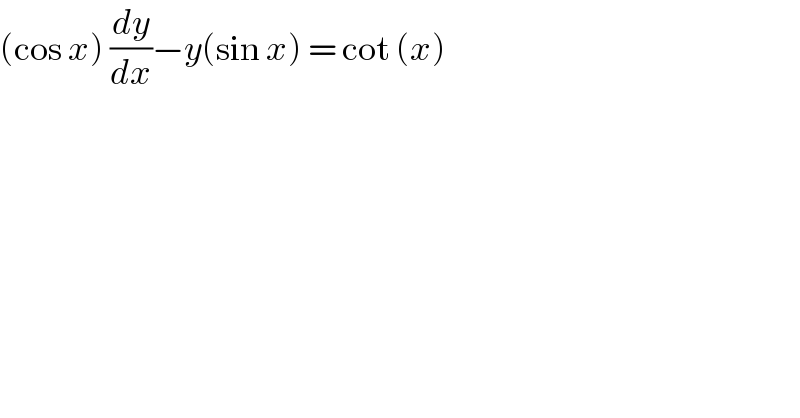
(cos x) (dy/dx)−y(sin x) = cot (x)

$$\left(\mathrm{cos}\:{x}\right)\:\frac{{dy}}{{dx}}−{y}\left(\mathrm{sin}\:{x}\right)\:=\:\mathrm{cot}\:\left({x}\right) \\ $$

Commented by Tony Lin last updated on 03/May/20

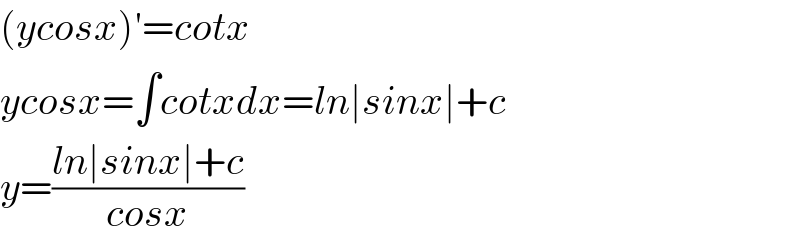
(ycosx)′=cotx ycosx=∫cotxdx=ln∣sinx∣+c y=((ln∣sinx∣+c)/(cosx))

$$\left({ycosx}\right)'={cotx} \\ $$$${ycosx}=\int{cotxdx}={ln}\mid{sinx}\mid+{c} \\ $$$${y}=\frac{{ln}\mid{sinx}\mid+{c}}{{cosx}} \\ $$

Commented by john santu last updated on 03/May/20

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Commented by mathmax by abdo last updated on 04/May/20

cosx y^′ −sinx y =cotanx (he) →cosx y^′ −sinx y =0 ⇒cosx y^′ =sinx y ⇒ (y^′ /y) =((sinx)/(cosx)) ⇒ln∣y∣ =−ln(cosx)+c ⇒y =(k/(cosx)) let use mvc method →y^′ =(k^′ /(cosx))+k((sinx)/(cos^2 x)) (e)⇒k^′ +k ((sinx)/(cosx))−((ksinx)/(cosx)) =(1/(tanx)) ⇒k^′ =((cosx)/(sinx)) ⇒ k =∫ ((cosx)/(sinx))dx +c ⇒k(x)=ln(sinx) +c ⇒ the general solution is y(x)=(1/(cosx))(ln(sinx) +c) =((ln(sinx))/(cosx)) +(c/(cosx))

$${cosx}\:{y}^{'} −{sinx}\:{y}\:={cotanx} \\ $$$$\left({he}\right)\:\rightarrow{cosx}\:{y}^{'} \:−{sinx}\:{y}\:=\mathrm{0}\:\Rightarrow{cosx}\:{y}^{'} \:={sinx}\:{y}\:\Rightarrow \\ $$$$\frac{{y}^{'} }{{y}}\:=\frac{{sinx}}{{cosx}}\:\Rightarrow{ln}\mid{y}\mid\:=−{ln}\left({cosx}\right)+{c}\:\Rightarrow{y}\:=\frac{{k}}{{cosx}} \\ $$$${let}\:{use}\:{mvc}\:{method}\:\:\rightarrow{y}^{'} \:=\frac{{k}^{'} }{{cosx}}+{k}\frac{{sinx}}{{cos}^{\mathrm{2}} {x}} \\ $$$$\left({e}\right)\Rightarrow{k}^{'} +{k}\:\frac{{sinx}}{{cosx}}−\frac{{ksinx}}{{cosx}}\:=\frac{\mathrm{1}}{{tanx}}\:\Rightarrow{k}^{'} \:=\frac{{cosx}}{{sinx}}\:\Rightarrow \\ $$$${k}\:=\int\:\:\frac{{cosx}}{{sinx}}{dx}\:+{c}\:\Rightarrow{k}\left({x}\right)={ln}\left({sinx}\right)\:+{c}\:\Rightarrow \\ $$$${the}\:{general}\:{solution}\:{is}\:{y}\left({x}\right)=\frac{\mathrm{1}}{{cosx}}\left({ln}\left({sinx}\right)\:+{c}\right) \\ $$$$=\frac{{ln}\left({sinx}\right)}{{cosx}}\:+\frac{{c}}{{cosx}} \\ $$

Answered by john santu last updated on 03/May/20

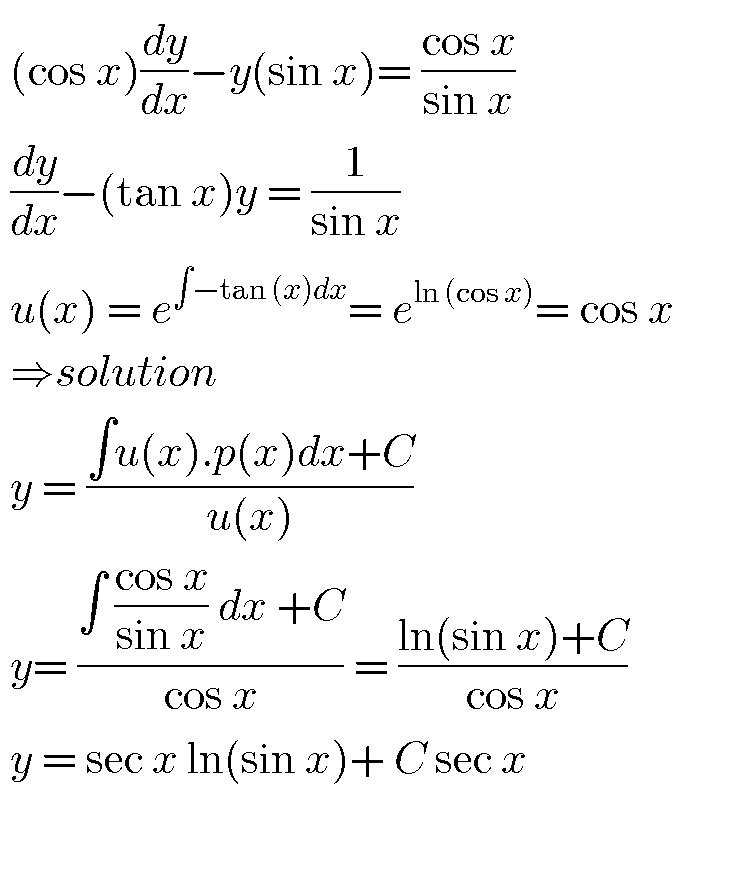
Commented by john santu last updated on 03/May/20

������

Answered by niroj last updated on 03/May/20

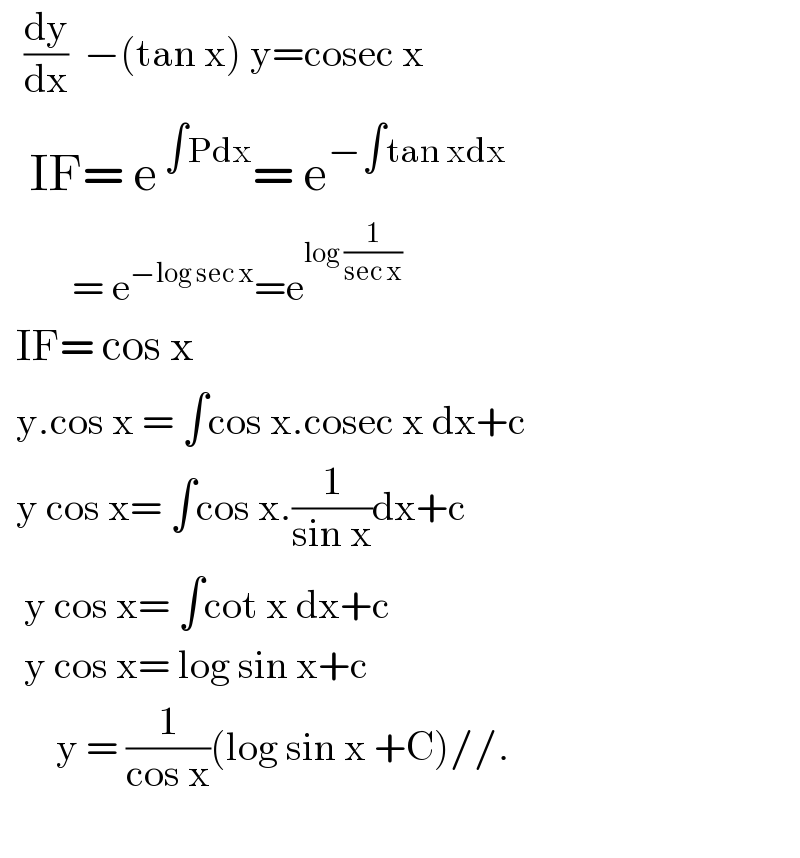
(dy/dx) −(tan x) y=cosec x IF= e^( ∫Pdx) = e^(−∫tan xdx) = e^(−log sec x) =e^(log (1/(sec x))) IF= cos x y.cos x = ∫cos x.cosec x dx+c y cos x= ∫cos x.(1/(sin x))dx+c y cos x= ∫cot x dx+c y cos x= log sin x+c y = (1/(cos x))(log sin x +C)//.

$$\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:\:−\left(\mathrm{tan}\:\mathrm{x}\right)\:\mathrm{y}=\mathrm{cosec}\:\mathrm{x} \\ $$$$\:\:\:\mathrm{IF}=\:\mathrm{e}^{\:\int\mathrm{Pdx}} =\:\mathrm{e}^{−\int\mathrm{tan}\:\mathrm{xdx}} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\mathrm{e}^{−\mathrm{log}\:\mathrm{sec}\:\mathrm{x}} =\mathrm{e}^{\mathrm{log}\:\frac{\mathrm{1}}{\mathrm{sec}\:\mathrm{x}}} \\ $$$$\:\:\mathrm{IF}=\:\mathrm{cos}\:\mathrm{x} \\ $$$$\:\:\mathrm{y}.\mathrm{cos}\:\mathrm{x}\:=\:\int\mathrm{cos}\:\mathrm{x}.\mathrm{cosec}\:\mathrm{x}\:\mathrm{dx}+\mathrm{c} \\ $$$$\:\:\mathrm{y}\:\mathrm{cos}\:\mathrm{x}=\:\int\mathrm{cos}\:\mathrm{x}.\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{x}}\mathrm{dx}+\mathrm{c} \\ $$$$\:\:\:\mathrm{y}\:\mathrm{cos}\:\mathrm{x}=\:\int\mathrm{cot}\:\mathrm{x}\:\mathrm{dx}+\mathrm{c} \\ $$$$\:\:\:\mathrm{y}\:\mathrm{cos}\:\mathrm{x}=\:\mathrm{log}\:\mathrm{sin}\:\mathrm{x}+\mathrm{c} \\ $$$$\:\:\:\:\:\:\:\mathrm{y}\:=\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{x}}\left(\mathrm{log}\:\mathrm{sin}\:\mathrm{x}\:+\mathrm{C}\right)//. \\ $$$$ \\ $$

Commented by john santu last updated on 03/May/20

����

Terms of Service

Privacy Policy

Contact: info@tinkutara.com