Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 115455 by bemath last updated on 26/Sep/20

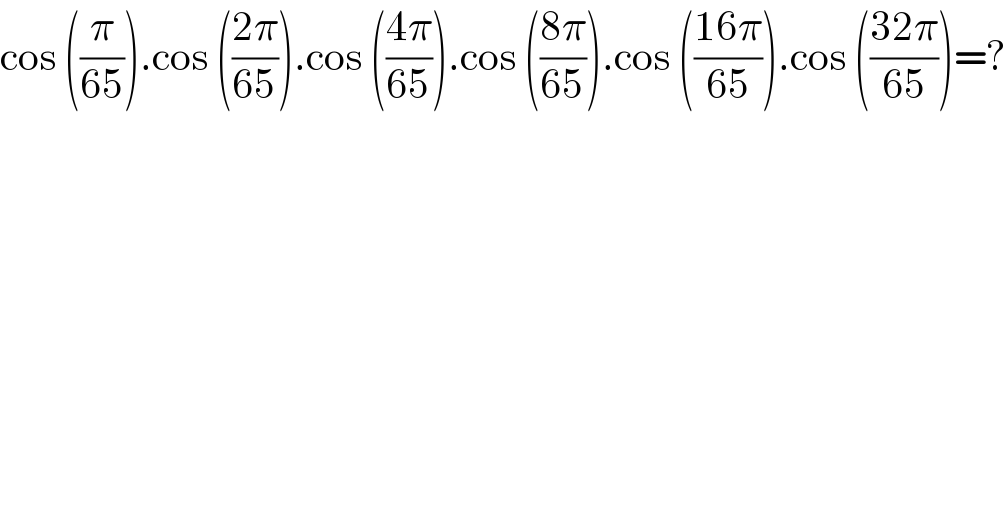
cos ((π/(65))).cos (((2π)/(65))).cos (((4π)/(65))).cos (((8π)/(65))).cos (((16π)/(65))).cos (((32π)/(65)))=?

$$\mathrm{cos}\:\left(\frac{\pi}{\mathrm{65}}\right).\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{65}}\right).\mathrm{cos}\:\left(\frac{\mathrm{4}\pi}{\mathrm{65}}\right).\mathrm{cos}\:\left(\frac{\mathrm{8}\pi}{\mathrm{65}}\right).\mathrm{cos}\:\left(\frac{\mathrm{16}\pi}{\mathrm{65}}\right).\mathrm{cos}\:\left(\frac{\mathrm{32}\pi}{\mathrm{65}}\right)=? \\ $$

Commented by Adel last updated on 13/Jan/21

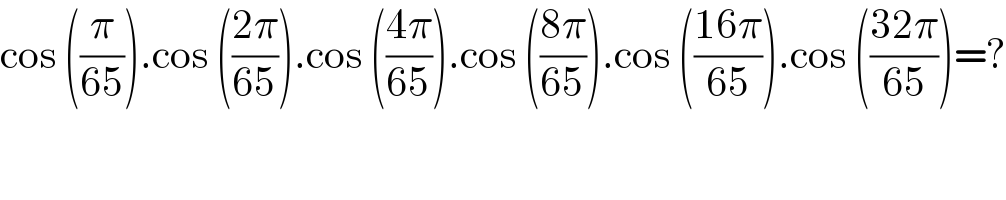
cos ((π/(65))).cos (((2π)/(65))).cos (((4π)/(65))).cos (((8π)/(65))).cos (((16π)/(65))).cos (((32π)/(65)))=?

$$\mathrm{cos}\:\left(\frac{\pi}{\mathrm{65}}\right).\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{65}}\right).\mathrm{cos}\:\left(\frac{\mathrm{4}\pi}{\mathrm{65}}\right).\mathrm{cos}\:\left(\frac{\mathrm{8}\pi}{\mathrm{65}}\right).\mathrm{cos}\:\left(\frac{\mathrm{16}\pi}{\mathrm{65}}\right).\mathrm{cos}\:\left(\frac{\mathrm{32}\pi}{\mathrm{65}}\right)=? \\ $$

Answered by TANMAY PANACEA last updated on 26/Sep/20

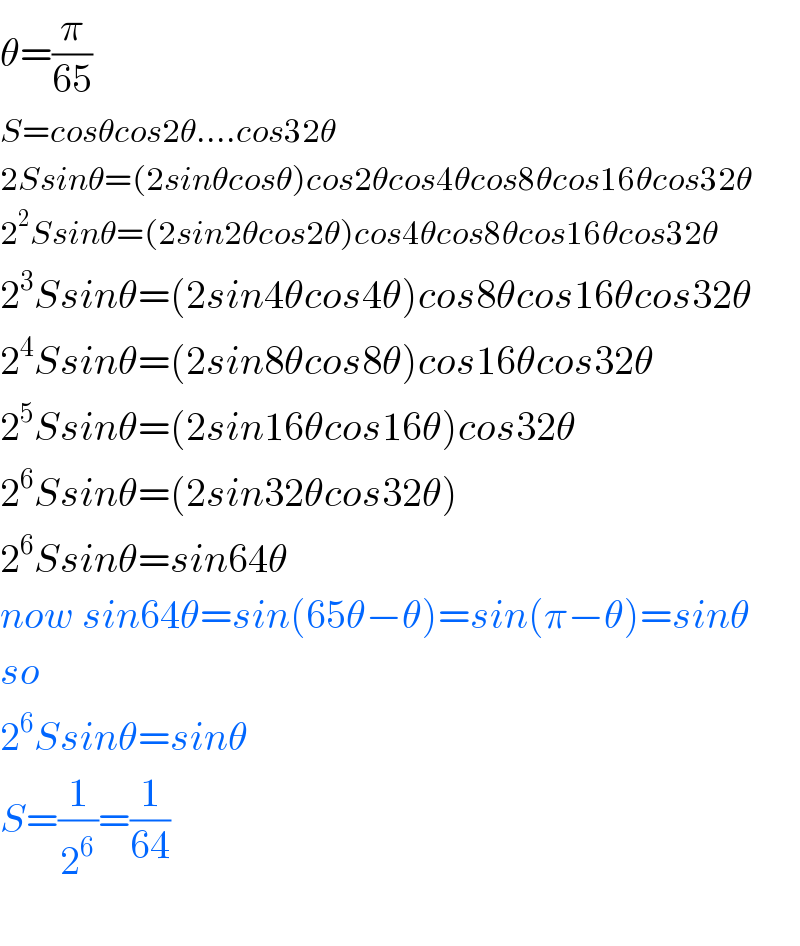
θ=(π/(65)) S=cosθcos2θ....cos32θ 2Ssinθ=(2sinθcosθ)cos2θcos4θcos8θcos16θcos32θ 2^2 Ssinθ=(2sin2θcos2θ)cos4θcos8θcos16θcos32θ 2^3 Ssinθ=(2sin4θcos4θ)cos8θcos16θcos32θ 2^4 Ssinθ=(2sin8θcos8θ)cos16θcos32θ 2^5 Ssinθ=(2sin16θcos16θ)cos32θ 2^6 Ssinθ=(2sin32θcos32θ) 2^6 Ssinθ=sin64θ now sin64θ=sin(65θ−θ)=sin(π−θ)=sinθ so 2^6 Ssinθ=sinθ S=(1/2^6 )=(1/(64))

$$\theta=\frac{\pi}{\mathrm{65}} \\ $$$${S}={cos}\theta{cos}\mathrm{2}\theta....{cos}\mathrm{32}\theta \\ $$$$\mathrm{2}{Ssin}\theta=\left(\mathrm{2}{sin}\theta{cos}\theta\right){cos}\mathrm{2}\theta{cos}\mathrm{4}\theta{cos}\mathrm{8}\theta{cos}\mathrm{16}\theta{cos}\mathrm{32}\theta \\ $$$$\mathrm{2}^{\mathrm{2}} {Ssin}\theta=\left(\mathrm{2}{sin}\mathrm{2}\theta{cos}\mathrm{2}\theta\right){cos}\mathrm{4}\theta{cos}\mathrm{8}\theta{cos}\mathrm{16}\theta{cos}\mathrm{32}\theta \\ $$$$\mathrm{2}^{\mathrm{3}} {Ssin}\theta=\left(\mathrm{2}{sin}\mathrm{4}\theta{cos}\mathrm{4}\theta\right){cos}\mathrm{8}\theta{cos}\mathrm{16}\theta{cos}\mathrm{32}\theta \\ $$$$\mathrm{2}^{\mathrm{4}} {Ssin}\theta=\left(\mathrm{2}{sin}\mathrm{8}\theta{cos}\mathrm{8}\theta\right){cos}\mathrm{16}\theta{cos}\mathrm{32}\theta \\ $$$$\mathrm{2}^{\mathrm{5}} {Ssin}\theta=\left(\mathrm{2}{sin}\mathrm{16}\theta{cos}\mathrm{16}\theta\right){cos}\mathrm{32}\theta \\ $$$$\mathrm{2}^{\mathrm{6}} {Ssin}\theta=\left(\mathrm{2}{sin}\mathrm{32}\theta{cos}\mathrm{32}\theta\right) \\ $$$$\mathrm{2}^{\mathrm{6}} {Ssin}\theta={sin}\mathrm{64}\theta \\ $$$${now}\:{sin}\mathrm{64}\theta={sin}\left(\mathrm{65}\theta−\theta\right)={sin}\left(\pi−\theta\right)={sin}\theta \\ $$$${so} \\ $$$$\mathrm{2}^{\mathrm{6}} {Ssin}\theta={sin}\theta \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{6}} }=\frac{\mathrm{1}}{\mathrm{64}} \\ $$$$ \\ $$

Commented by bemath last updated on 26/Sep/20

santuyy...gave kudos

$${santuyy}...{gave}\:{kudos} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com