Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 73757 by Maclaurin Stickker last updated on 15/Nov/19

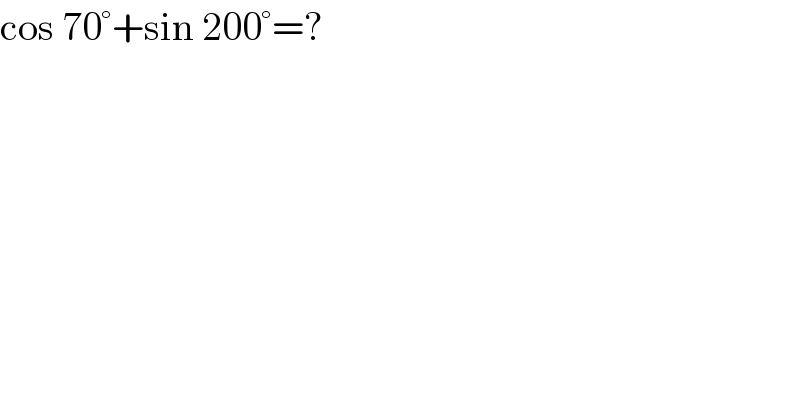
cos 70°+sin 200°=?

$$\mathrm{cos}\:\mathrm{70}°+\mathrm{sin}\:\mathrm{200}°=? \\ $$

Commented by mathmax by abdo last updated on 15/Nov/19

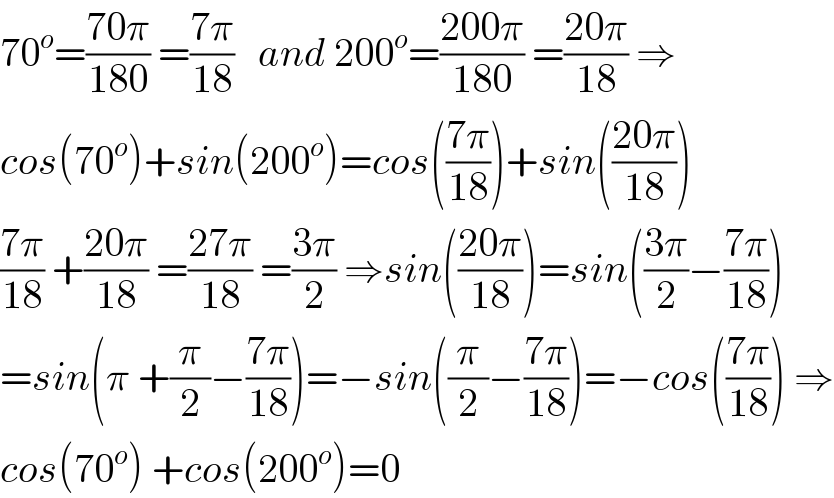
70^o =((70π)/(180)) =((7π)/(18)) and 200^o =((200π)/(180)) =((20π)/(18)) ⇒ cos(70^o )+sin(200^o )=cos(((7π)/(18)))+sin(((20π)/(18))) ((7π)/(18)) +((20π)/(18)) =((27π)/(18)) =((3π)/2) ⇒sin(((20π)/(18)))=sin(((3π)/2)−((7π)/(18))) =sin(π +(π/2)−((7π)/(18)))=−sin((π/2)−((7π)/(18)))=−cos(((7π)/(18))) ⇒ cos(70^o ) +cos(200^o )=0

$$\mathrm{70}^{{o}} =\frac{\mathrm{70}\pi}{\mathrm{180}}\:=\frac{\mathrm{7}\pi}{\mathrm{18}}\:\:\:{and}\:\mathrm{200}^{{o}} =\frac{\mathrm{200}\pi}{\mathrm{180}}\:=\frac{\mathrm{20}\pi}{\mathrm{18}}\:\Rightarrow \\ $$$${cos}\left(\mathrm{70}^{{o}} \right)+{sin}\left(\mathrm{200}^{{o}} \right)={cos}\left(\frac{\mathrm{7}\pi}{\mathrm{18}}\right)+{sin}\left(\frac{\mathrm{20}\pi}{\mathrm{18}}\right) \\ $$$$\frac{\mathrm{7}\pi}{\mathrm{18}}\:+\frac{\mathrm{20}\pi}{\mathrm{18}}\:=\frac{\mathrm{27}\pi}{\mathrm{18}}\:=\frac{\mathrm{3}\pi}{\mathrm{2}}\:\Rightarrow{sin}\left(\frac{\mathrm{20}\pi}{\mathrm{18}}\right)={sin}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}−\frac{\mathrm{7}\pi}{\mathrm{18}}\right) \\ $$$$={sin}\left(\pi\:+\frac{\pi}{\mathrm{2}}−\frac{\mathrm{7}\pi}{\mathrm{18}}\right)=−{sin}\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{7}\pi}{\mathrm{18}}\right)=−{cos}\left(\frac{\mathrm{7}\pi}{\mathrm{18}}\right)\:\Rightarrow \\ $$$${cos}\left(\mathrm{70}^{{o}} \right)\:+{cos}\left(\mathrm{200}^{{o}} \right)=\mathrm{0} \\ $$

Answered by ajfour last updated on 15/Nov/19

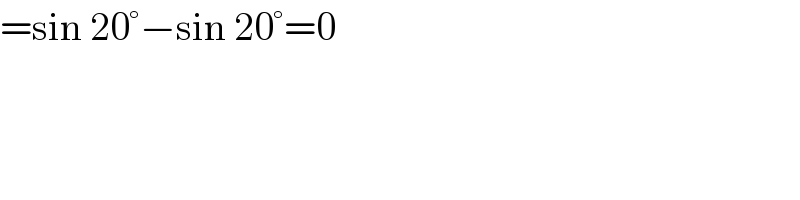
=sin 20°−sin 20°=0

$$=\mathrm{sin}\:\mathrm{20}°−\mathrm{sin}\:\mathrm{20}°=\mathrm{0} \\ $$

Commented by Maclaurin Stickker last updated on 15/Nov/19

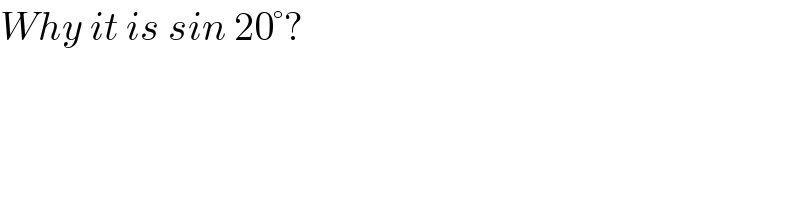
Why it is sin 20°?

$${Why}\:{it}\:{is}\:{sin}\:\mathrm{20}°? \\ $$

Commented by ajfour last updated on 15/Nov/19

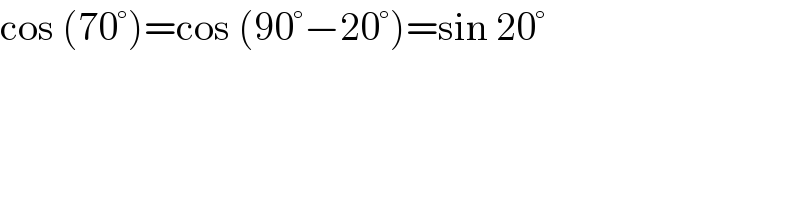
cos (70°)=cos (90°−20°)=sin 20°

$$\mathrm{cos}\:\left(\mathrm{70}°\right)=\mathrm{cos}\:\left(\mathrm{90}°−\mathrm{20}°\right)=\mathrm{sin}\:\mathrm{20}° \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com