Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 121203 by benjo_mathlover last updated on 05/Nov/20

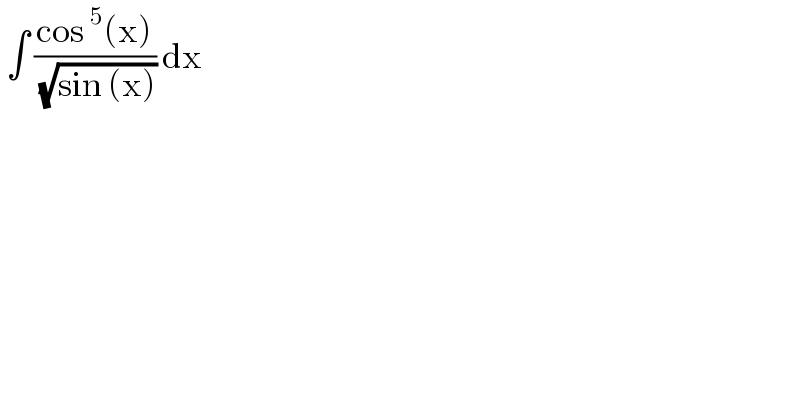
∫ ((cos^5 (x))/( (√(sin (x))))) dx

$$\:\int\:\frac{\mathrm{cos}\:^{\mathrm{5}} \left(\mathrm{x}\right)}{\:\sqrt{\mathrm{sin}\:\left(\mathrm{x}\right)}}\:\mathrm{dx}\: \\ $$

Answered by MJS_new last updated on 06/Nov/20

∫((cos^5 x)/( (√(sin x))))dx= [t=(√(sin x)) → dx=((2(√(sin x)))/(cos x))dt] =2∫(t^4 −1)^2 dt= =(2/9)t^9 −(4/5)t^5 +2t= =2((1/9)sin^4 x −(2/5)sin^2 x +1)(√(sin x)) +C

$$\int\frac{\mathrm{cos}^{\mathrm{5}} \:{x}}{\:\sqrt{\mathrm{sin}\:{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{sin}\:{x}}\:\rightarrow\:{dx}=\frac{\mathrm{2}\sqrt{\mathrm{sin}\:{x}}}{\mathrm{cos}\:{x}}{dt}\right] \\ $$$$=\mathrm{2}\int\left({t}^{\mathrm{4}} −\mathrm{1}\right)^{\mathrm{2}} {dt}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{9}}{t}^{\mathrm{9}} −\frac{\mathrm{4}}{\mathrm{5}}{t}^{\mathrm{5}} +\mathrm{2}{t}= \\ $$$$=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{9}}\mathrm{sin}^{\mathrm{4}} \:{x}\:−\frac{\mathrm{2}}{\mathrm{5}}\mathrm{sin}^{\mathrm{2}} \:{x}\:+\mathrm{1}\right)\sqrt{\mathrm{sin}\:{x}}\:+{C} \\ $$

Answered by bobhans last updated on 06/Nov/20

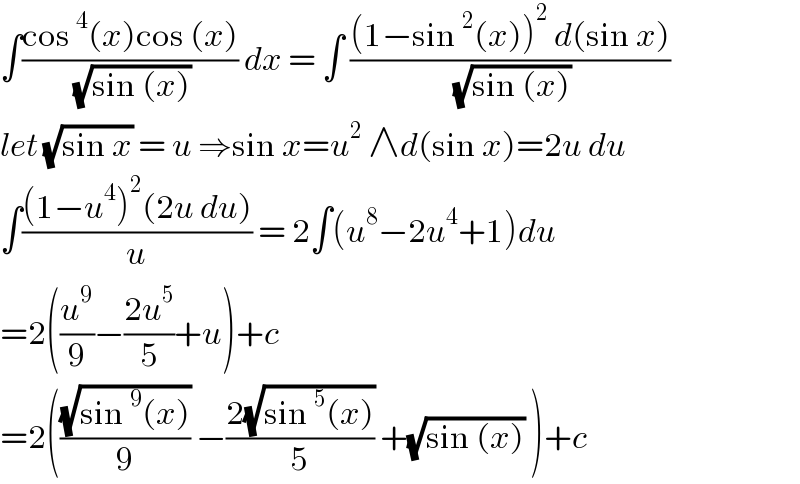
∫((cos^4 (x)cos (x))/( (√(sin (x))))) dx = ∫ (((1−sin^2 (x))^2 d(sin x))/( (√(sin (x))))) let (√(sin x)) = u ⇒sin x=u^2 ∧d(sin x)=2u du ∫(((1−u^4 )^2 (2u du))/u) = 2∫(u^8 −2u^4 +1)du =2((u^9 /9)−((2u^5 )/5)+u)+c =2(((√(sin^9 (x)))/9) −((2(√(sin^5 (x))))/5) +(√(sin (x))) )+c

$$\int\frac{\mathrm{cos}\:^{\mathrm{4}} \left({x}\right)\mathrm{cos}\:\left({x}\right)}{\:\sqrt{\mathrm{sin}\:\left({x}\right)}}\:{dx}\:=\:\int\:\frac{\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \left({x}\right)\right)^{\mathrm{2}} \:{d}\left(\mathrm{sin}\:{x}\right)}{\:\sqrt{\mathrm{sin}\:\left({x}\right)}} \\ $$$${let}\:\sqrt{\mathrm{sin}\:{x}}\:=\:{u}\:\Rightarrow\mathrm{sin}\:{x}={u}^{\mathrm{2}} \:\wedge{d}\left(\mathrm{sin}\:{x}\right)=\mathrm{2}{u}\:{du} \\ $$$$\int\frac{\left(\mathrm{1}−{u}^{\mathrm{4}} \right)^{\mathrm{2}} \left(\mathrm{2}{u}\:{du}\right)}{{u}}\:=\:\mathrm{2}\int\left({u}^{\mathrm{8}} −\mathrm{2}{u}^{\mathrm{4}} +\mathrm{1}\right){du} \\ $$$$=\mathrm{2}\left(\frac{{u}^{\mathrm{9}} }{\mathrm{9}}−\frac{\mathrm{2}{u}^{\mathrm{5}} }{\mathrm{5}}+{u}\right)+{c} \\ $$$$=\mathrm{2}\left(\frac{\sqrt{\mathrm{sin}\:^{\mathrm{9}} \left({x}\right)}}{\mathrm{9}}\:−\frac{\mathrm{2}\sqrt{\mathrm{sin}\:^{\mathrm{5}} \left({x}\right)}}{\mathrm{5}}\:+\sqrt{\mathrm{sin}\:\left({x}\right)}\:\right)+{c} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com