Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 29111 by gyugfeet last updated on 04/Feb/18

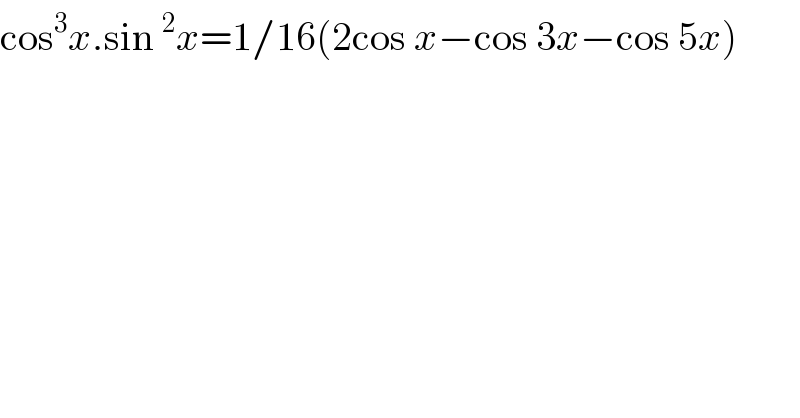
cos^3 x.sin^2 x=1/16(2cos x−cos 3x−cos 5x)

$$\mathrm{cos}^{\mathrm{3}} {x}.\mathrm{sin}\:^{\mathrm{2}} {x}=\mathrm{1}/\mathrm{16}\left(\mathrm{2cos}\:{x}−\mathrm{cos}\:\mathrm{3}{x}−\mathrm{cos}\:\mathrm{5}{x}\right) \\ $$

Commented by abdo imad last updated on 04/Feb/18

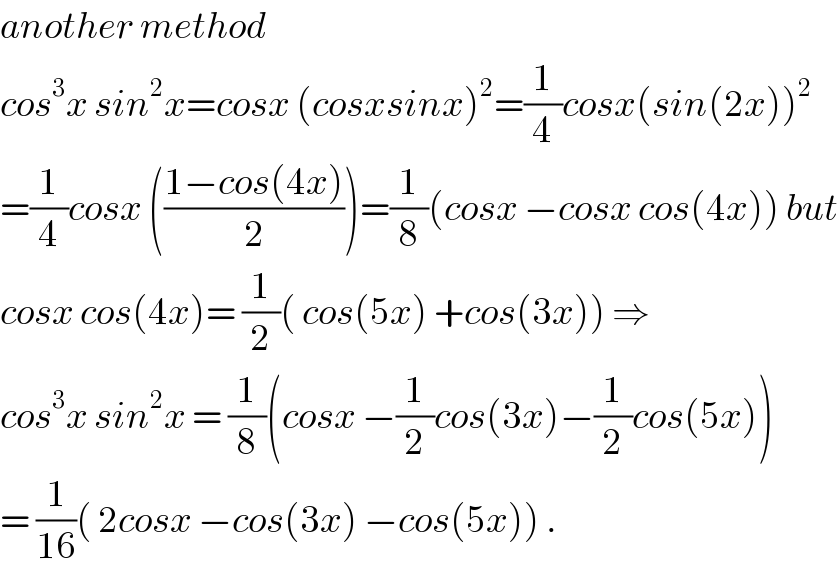
another method cos^3 x sin^2 x=cosx (cosxsinx)^2 =(1/4)cosx(sin(2x))^2 =(1/4)cosx (((1−cos(4x))/2))=(1/8)(cosx −cosx cos(4x)) but cosx cos(4x)= (1/2)( cos(5x) +cos(3x)) ⇒ cos^3 x sin^2 x = (1/8)(cosx −(1/2)cos(3x)−(1/2)cos(5x)) = (1/(16))( 2cosx −cos(3x) −cos(5x)) .

$${another}\:{method} \\ $$$${cos}^{\mathrm{3}} {x}\:{sin}^{\mathrm{2}} {x}={cosx}\:\left({cosxsinx}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}{cosx}\left({sin}\left(\mathrm{2}{x}\right)\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{cosx}\:\left(\frac{\mathrm{1}−{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{8}}\left({cosx}\:−{cosx}\:{cos}\left(\mathrm{4}{x}\right)\right)\:{but} \\ $$$${cosx}\:{cos}\left(\mathrm{4}{x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\:{cos}\left(\mathrm{5}{x}\right)\:+{cos}\left(\mathrm{3}{x}\right)\right)\:\Rightarrow \\ $$$${cos}^{\mathrm{3}} {x}\:{sin}^{\mathrm{2}} {x}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left({cosx}\:−\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\mathrm{3}{x}\right)−\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\mathrm{5}{x}\right)\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{16}}\left(\:\mathrm{2}{cosx}\:−{cos}\left(\mathrm{3}{x}\right)\:−{cos}\left(\mathrm{5}{x}\right)\right)\:. \\ $$

Answered by ajfour last updated on 04/Feb/18

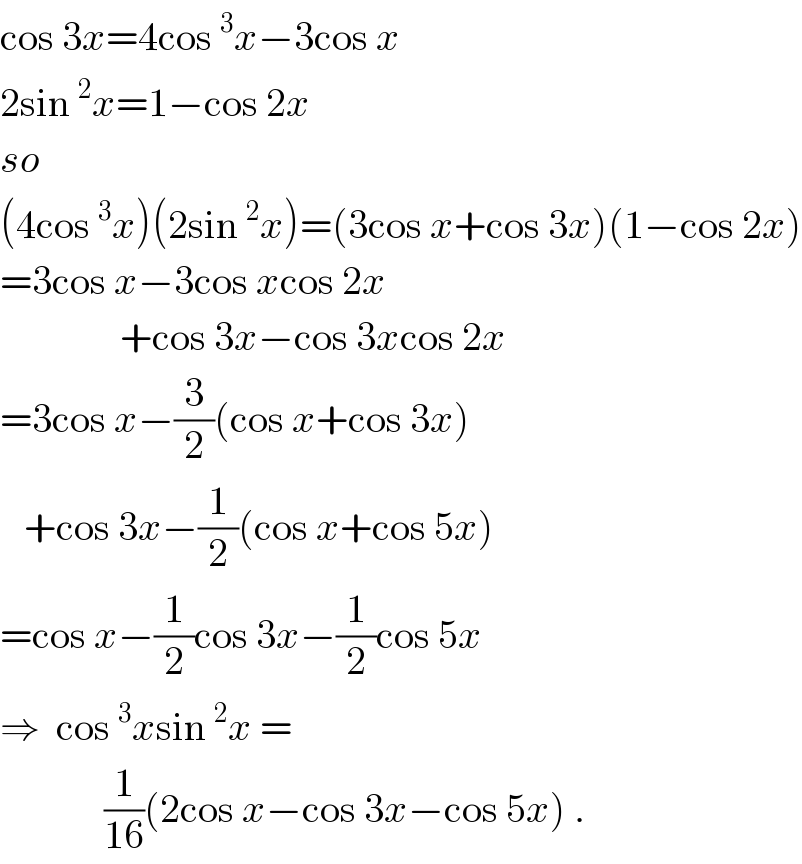
cos 3x=4cos^3 x−3cos x 2sin^2 x=1−cos 2x so (4cos^3 x)(2sin^2 x)=(3cos x+cos 3x)(1−cos 2x) =3cos x−3cos xcos 2x +cos 3x−cos 3xcos 2x =3cos x−(3/2)(cos x+cos 3x) +cos 3x−(1/2)(cos x+cos 5x) =cos x−(1/2)cos 3x−(1/2)cos 5x ⇒ cos^3 xsin^2 x = (1/(16))(2cos x−cos 3x−cos 5x) .

$$\mathrm{cos}\:\mathrm{3}{x}=\mathrm{4cos}\:^{\mathrm{3}} {x}−\mathrm{3cos}\:{x} \\ $$$$\mathrm{2sin}\:^{\mathrm{2}} {x}=\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x} \\ $$$${so} \\ $$$$\left(\mathrm{4cos}\:^{\mathrm{3}} {x}\right)\left(\mathrm{2sin}\:^{\mathrm{2}} {x}\right)=\left(\mathrm{3cos}\:{x}+\mathrm{cos}\:\mathrm{3}{x}\right)\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right) \\ $$$$=\mathrm{3cos}\:{x}−\mathrm{3cos}\:{x}\mathrm{cos}\:\mathrm{2}{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{cos}\:\mathrm{3}{x}−\mathrm{cos}\:\mathrm{3}{x}\mathrm{cos}\:\mathrm{2}{x} \\ $$$$=\mathrm{3cos}\:{x}−\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{cos}\:{x}+\mathrm{cos}\:\mathrm{3}{x}\right) \\ $$$$\:\:\:+\mathrm{cos}\:\mathrm{3}{x}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:{x}+\mathrm{cos}\:\mathrm{5}{x}\right) \\ $$$$=\mathrm{cos}\:{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{3}{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{5}{x} \\ $$$$\Rightarrow\:\:\mathrm{cos}\:^{\mathrm{3}} {x}\mathrm{sin}\:^{\mathrm{2}} {x}\:= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{2cos}\:{x}−\mathrm{cos}\:\mathrm{3}{x}−\mathrm{cos}\:\mathrm{5}{x}\right)\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com