Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 145064 by akolade last updated on 02/Jul/21

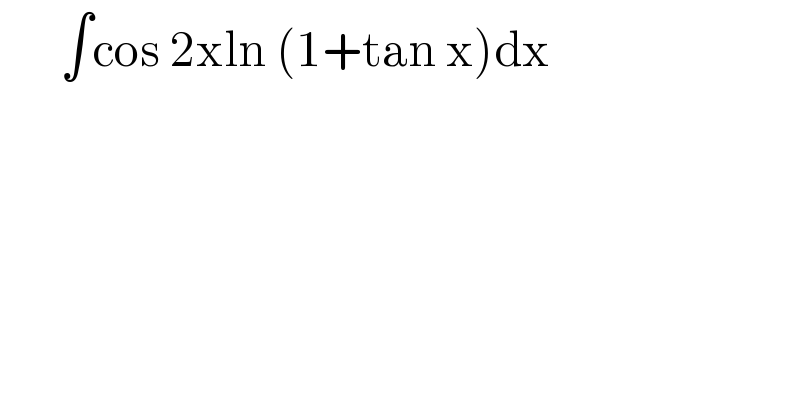
∫cos 2xln (1+tan x)dx

$$\:\:\:\:\:\:\int\mathrm{cos}\:\mathrm{2xln}\:\left(\mathrm{1}+\mathrm{tan}\:\mathrm{x}\right)\mathrm{dx} \\ $$$$\:\:\:\:\:\: \\ $$

Answered by mathmax by abdo last updated on 02/Jul/21

Ψ=∫ cos(2x)log(1+tanx)dx by parts Ψ=((sin(2x))/2)log(1+tanx)−∫((sin(2x))/2)×(((1+tan^2 x))/(1+tanx))dx ∫ sin(2x).((1+tan^2 x)/(1+tanx))dx =_(tanx=t) ∫((2t)/(1+t^2 ))×((1+t^2 )/(1+t))(dt/(1+t^2 )) =2∫ (t/((t+1)(t^2 +1)))dt let decompose F(t)=(t/((t+1)(t^2 +1))) F(t)=(a/(t+1))+((bt+c)/(t^2 +1)) ⇒a=−(1/2) lim_(t→+∞) tF(t)=0=a+b ⇒b=(1/2) F(0)=0=a+c ⇒c=(1/2) ⇒F(t)=((−1)/(2(t+1)))+(1/2)×((t+1)/(t^2 +1))⇒ ∫ F(t)dt=−(1/2)log∣t+1∣+(1/4)log(t^2 +1)+(1/2)arctant +K ⇒ Ψ=(1/2)sin(2x)log(1+tanx)+(1/2)log∣tanx+1∣−(1/4)log(1+tan^2 x)+(x/2)+K

$$\Psi=\int\:\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{log}\left(\mathrm{1}+\mathrm{tanx}\right)\mathrm{dx}\:\:\:\mathrm{by}\:\mathrm{parts} \\ $$$$\Psi=\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2}}\mathrm{log}\left(\mathrm{1}+\mathrm{tanx}\right)−\int\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2}}×\frac{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{1}+\mathrm{tanx}}\mathrm{dx} \\ $$$$\int\:\mathrm{sin}\left(\mathrm{2x}\right).\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}+\mathrm{tanx}}\mathrm{dx}\:\:=_{\mathrm{tanx}=\mathrm{t}} \:\:\:\int\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }×\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}}\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int\:\frac{\mathrm{t}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dt}\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{t}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{a}}{\mathrm{t}+\mathrm{1}}+\frac{\mathrm{bt}+\mathrm{c}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{a}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)=\mathrm{0}=\mathrm{a}+\mathrm{b}\:\Rightarrow\mathrm{b}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{F}\left(\mathrm{0}\right)=\mathrm{0}=\mathrm{a}+\mathrm{c}\:\Rightarrow\mathrm{c}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)=\frac{−\mathrm{1}}{\mathrm{2}\left(\mathrm{t}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{t}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\Rightarrow \\ $$$$\int\:\mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\mid\mathrm{t}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctant}\:+\mathrm{K}\:\Rightarrow \\ $$$$\Psi=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)\mathrm{log}\left(\mathrm{1}+\mathrm{tanx}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\mid\mathrm{tanx}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)+\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{K} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com