
Question Number 217122 by efronzo1 last updated on 01/Mar/25
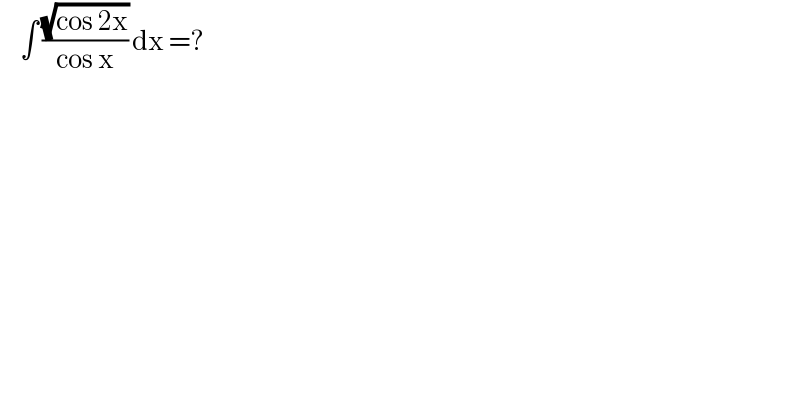
$$\:\:\:\:\:\int\:\frac{\sqrt{\mathrm{cos}\:\mathrm{2x}}}{\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx}\:=? \\ $$
Answered by Frix last updated on 01/Mar/25
![∫((√(cos 2x))/(cos x))dx=∫((√(−1+2cos^2 x))/(cos x))dx =^([t=(√2)sin x]) =(√2)∫((√(1−t^2 ))/(2−t^2 ))dt =^([u=(t/( (√(1−t^2 ))))]) (√2)∫(du/((u^2 +1)(u^2 +2)))= =(√2)∫((1/(u^2 +1))−(1/(u^2 +2)))du= =(√2)tan^(−1) u −tan^(−1) (u/( (√2))) = ... =(√2)sin^(−1) ((√2)sin x) −sin^(−1) (tan x) +C](Q217123.png)
$$\int\frac{\sqrt{\mathrm{cos}\:\mathrm{2}{x}}}{\mathrm{cos}\:{x}}{dx}=\int\frac{\sqrt{−\mathrm{1}+\mathrm{2cos}^{\mathrm{2}} \:{x}}}{\mathrm{cos}\:{x}}{dx}\:\overset{\left[{t}=\sqrt{\mathrm{2}}\mathrm{sin}\:{x}\right]} {=} \\ $$$$=\sqrt{\mathrm{2}}\int\frac{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{2}−{t}^{\mathrm{2}} }{dt}\:\overset{\left[{u}=\frac{{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\right]} {=}\:\sqrt{\mathrm{2}}\int\frac{{du}}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)\left({u}^{\mathrm{2}} +\mathrm{2}\right)}= \\ $$$$=\sqrt{\mathrm{2}}\int\left(\frac{\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{2}}\right){du}= \\ $$$$=\sqrt{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \:{u}\:−\mathrm{tan}^{−\mathrm{1}} \:\frac{{u}}{\:\sqrt{\mathrm{2}}}\:= \\ $$$$... \\ $$$$=\sqrt{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \:\left(\sqrt{\mathrm{2}}\mathrm{sin}\:{x}\right)\:−\mathrm{sin}^{−\mathrm{1}} \:\left(\mathrm{tan}\:{x}\right)\:+{C} \\ $$
