
Question Number 201728 by hardmath last updated on 11/Dec/23
![cos^2 4x ∙ sin^2 4x = 0,25 for equation [0;90] how many roots are there in the piece?](Q201728.png)
$$\mathrm{cos}^{\mathrm{2}} \:\mathrm{4x}\:\centerdot\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{4x}\:=\:\mathrm{0},\mathrm{25}\:\mathrm{for}\:\mathrm{equation} \\ $$$$\left[\mathrm{0};\mathrm{90}\right]\:\mathrm{how}\:\mathrm{many}\:\mathrm{roots}\:\mathrm{are}\:\mathrm{there}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{piece}? \\ $$
Answered by esmaeil last updated on 11/Dec/23
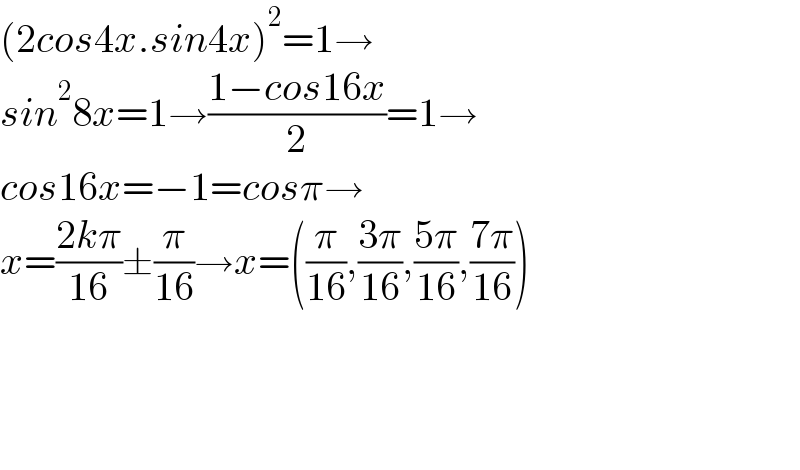
$$\left(\mathrm{2}{cos}\mathrm{4}{x}.{sin}\mathrm{4}{x}\right)^{\mathrm{2}} =\mathrm{1}\rightarrow \\ $$$${sin}^{\mathrm{2}} \mathrm{8}{x}=\mathrm{1}\rightarrow\frac{\mathrm{1}−{cos}\mathrm{16}{x}}{\mathrm{2}}=\mathrm{1}\rightarrow \\ $$$${cos}\mathrm{16}{x}=−\mathrm{1}={cos}\pi\rightarrow \\ $$$${x}=\frac{\mathrm{2}{k}\pi}{\mathrm{16}}\pm\frac{\pi}{\mathrm{16}}\rightarrow{x}=\left(\frac{\pi}{\mathrm{16}},\frac{\mathrm{3}\pi}{\mathrm{16}},\frac{\mathrm{5}\pi}{\mathrm{16}},\frac{\mathrm{7}\pi}{\mathrm{16}}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by hardmath last updated on 11/Dec/23
![thank you dear professor, i.e. the piece [0;90] has four roots ? answer: 4 ?](Q201738.png)
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor}, \\ $$$$\mathrm{i}.\mathrm{e}.\:\mathrm{the}\:\mathrm{piece}\:\left[\mathrm{0};\mathrm{90}\right]\:\mathrm{has}\:\mathrm{four}\:\mathrm{roots}\:? \\ $$$$\mathrm{answer}:\:\mathrm{4}\:? \\ $$
Commented by esmaeil last updated on 11/Dec/23

$${yes} \\ $$
Commented by esmaeil last updated on 11/Dec/23

$$\frac{\mathrm{2}{k}−\mathrm{1}}{\mathrm{16}}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{k}\leqslant\mathrm{4} \\ $$
