
Question Number 105650 by bemath last updated on 30/Jul/20
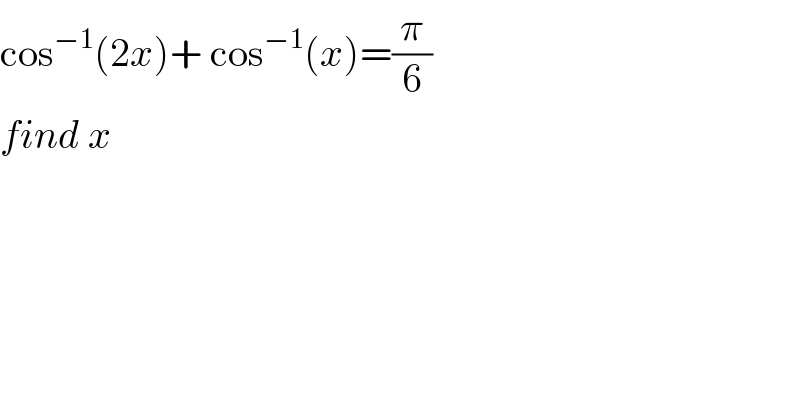
$$\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{2}{x}\right)+\:\mathrm{cos}^{−\mathrm{1}} \left({x}\right)=\frac{\pi}{\mathrm{6}} \\ $$$${find}\:{x} \\ $$
Answered by bramlex last updated on 30/Jul/20
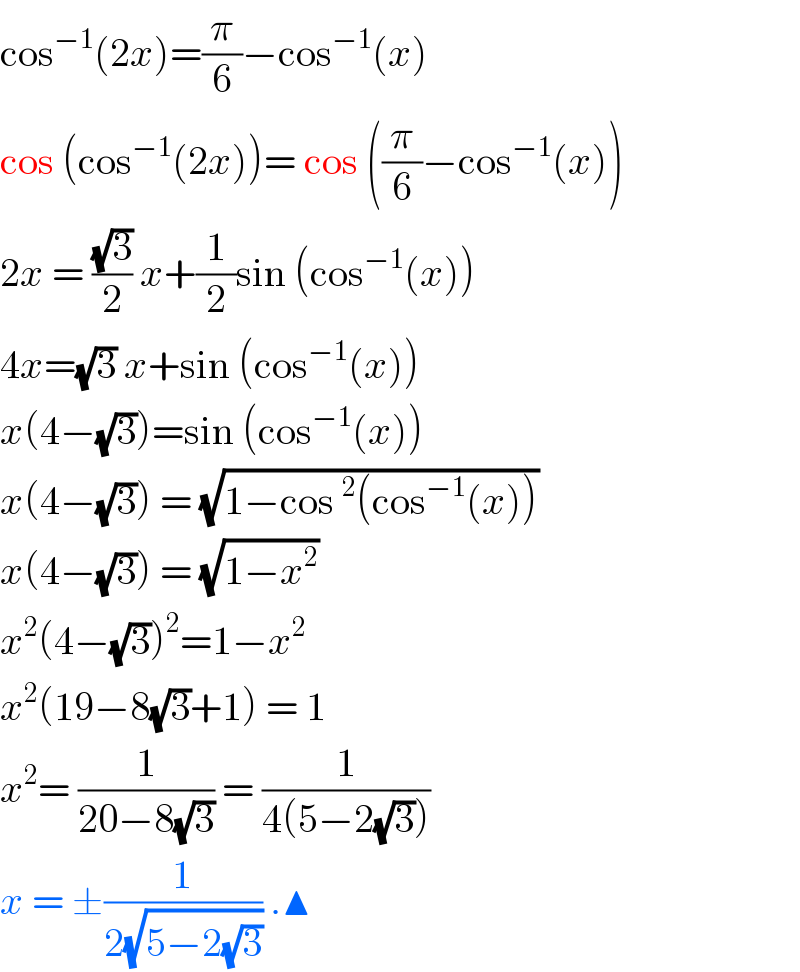
$$\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{2}{x}\right)=\frac{\pi}{\mathrm{6}}−\mathrm{cos}^{−\mathrm{1}} \left({x}\right) \\ $$$$\mathrm{cos}\:\left(\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{2}{x}\right)\right)=\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}−\mathrm{cos}^{−\mathrm{1}} \left({x}\right)\right) \\ $$$$\mathrm{2}{x}\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\left(\mathrm{cos}^{−\mathrm{1}} \left({x}\right)\right) \\ $$$$\mathrm{4}{x}=\sqrt{\mathrm{3}}\:{x}+\mathrm{sin}\:\left(\mathrm{cos}^{−\mathrm{1}} \left({x}\right)\right) \\ $$$${x}\left(\mathrm{4}−\sqrt{\mathrm{3}}\right)=\mathrm{sin}\:\left(\mathrm{cos}^{−\mathrm{1}} \left({x}\right)\right) \\ $$$${x}\left(\mathrm{4}−\sqrt{\mathrm{3}}\right)\:=\:\sqrt{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{cos}^{−\mathrm{1}} \left({x}\right)\right)} \\ $$$${x}\left(\mathrm{4}−\sqrt{\mathrm{3}}\right)\:=\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} \left(\mathrm{4}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} =\mathrm{1}−{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{19}−\mathrm{8}\sqrt{\mathrm{3}}+\mathrm{1}\right)\:=\:\mathrm{1} \\ $$$${x}^{\mathrm{2}} =\:\frac{\mathrm{1}}{\mathrm{20}−\mathrm{8}\sqrt{\mathrm{3}}}\:=\:\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{3}}\right)} \\ $$$${x}\:=\:\pm\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{3}}}}\:.\blacktriangle \\ $$
Answered by mathmax by abdo last updated on 31/Jul/20

$$\Rightarrow\mathrm{cos}\left(\mathrm{arcos}\left(\mathrm{2x}\right)+\mathrm{cosx}\right)\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{2x}\:.\mathrm{x}\:−\mathrm{sin}\left(\mathrm{arcos}\left(\mathrm{2x}\right)\right)\mathrm{sin}\left(\mathrm{cosx}\right)\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{2x}^{\mathrm{2}} −\sqrt{\mathrm{1}−\left(\mathrm{2x}\right)^{\mathrm{2}} }×\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow \\ $$$$\left(\mathrm{2x}^{\mathrm{2}} −\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:=\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }×\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\left(\mathrm{2x}^{\mathrm{2}} −\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} \:=\left(\mathrm{1}−\mathrm{4x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\mathrm{4x}^{\mathrm{4}} −\mathrm{2}\sqrt{\mathrm{3}}\mathrm{x}^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}\:=\mathrm{1}−\mathrm{x}^{\mathrm{2}} −\mathrm{4x}^{\mathrm{2}} +\mathrm{4x}^{\mathrm{4}} \:\Rightarrow \\ $$$$−\mathrm{2}\sqrt{\mathrm{3}}\mathrm{x}^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}\:=\mathrm{1}−\mathrm{5x}^{\mathrm{2}} \:\Rightarrow−\mathrm{8}\sqrt{\mathrm{3}}\mathrm{x}^{\mathrm{2}} +\mathrm{3}\:=\mathrm{4}−\mathrm{20x}^{\mathrm{2}} \:\Rightarrow \\ $$$$\left(\mathrm{20}−\mathrm{8}\sqrt{\mathrm{3}}\right)\mathrm{x}^{\mathrm{2}} \:=−\mathrm{3}\:\Rightarrow\left(\mathrm{8}\sqrt{\mathrm{3}}−\mathrm{20}\right)\mathrm{x}^{\mathrm{2}} \:=\mathrm{3}\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:=\frac{\mathrm{3}}{\mathrm{8}\sqrt{\mathrm{3}}−\mathrm{20}}\:\Rightarrow \\ $$$$\mathrm{x}\:=\overset{−} {+}\sqrt{\frac{\mathrm{3}}{\mathrm{8}\sqrt{\mathrm{3}}−\mathrm{20}}} \\ $$
