
Question Number 12533 by tawa last updated on 24/Apr/17
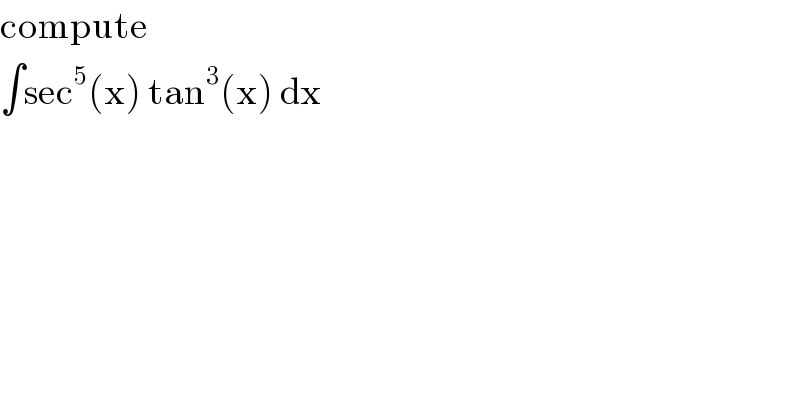
$$\mathrm{compute} \\ $$$$\int\mathrm{sec}^{\mathrm{5}} \left(\mathrm{x}\right)\:\mathrm{tan}^{\mathrm{3}} \left(\mathrm{x}\right)\:\mathrm{dx} \\ $$
Answered by sma3l2996 last updated on 25/Apr/17
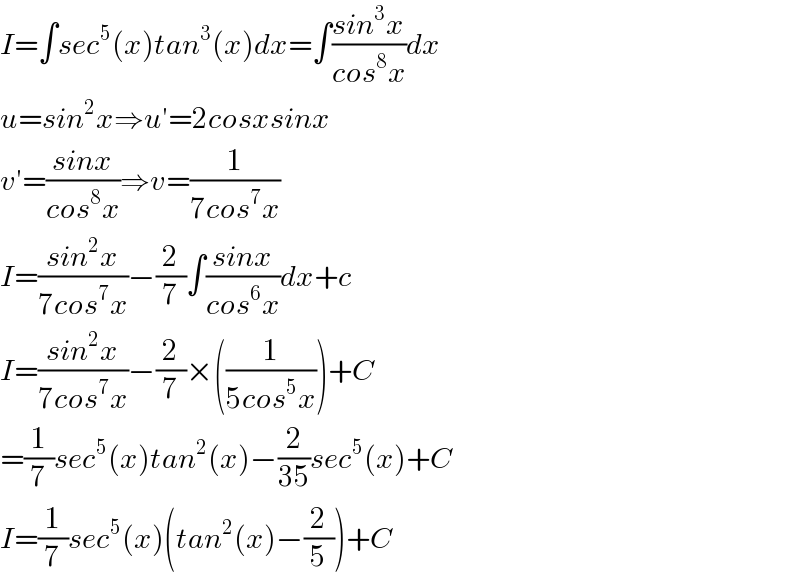
$${I}=\int{sec}^{\mathrm{5}} \left({x}\right){tan}^{\mathrm{3}} \left({x}\right){dx}=\int\frac{{sin}^{\mathrm{3}} {x}}{{cos}^{\mathrm{8}} {x}}{dx} \\ $$$${u}={sin}^{\mathrm{2}} {x}\Rightarrow{u}'=\mathrm{2}{cosxsinx} \\ $$$${v}'=\frac{{sinx}}{{cos}^{\mathrm{8}} {x}}\Rightarrow{v}=\frac{\mathrm{1}}{\mathrm{7}{cos}^{\mathrm{7}} {x}} \\ $$$${I}=\frac{{sin}^{\mathrm{2}} {x}}{\mathrm{7}{cos}^{\mathrm{7}} {x}}−\frac{\mathrm{2}}{\mathrm{7}}\int\frac{{sinx}}{{cos}^{\mathrm{6}} {x}}{dx}+{c} \\ $$$${I}=\frac{{sin}^{\mathrm{2}} {x}}{\mathrm{7}{cos}^{\mathrm{7}} {x}}−\frac{\mathrm{2}}{\mathrm{7}}×\left(\frac{\mathrm{1}}{\mathrm{5}{cos}^{\mathrm{5}} {x}}\right)+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}}{sec}^{\mathrm{5}} \left({x}\right){tan}^{\mathrm{2}} \left({x}\right)−\frac{\mathrm{2}}{\mathrm{35}}{sec}^{\mathrm{5}} \left({x}\right)+{C} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{7}}{sec}^{\mathrm{5}} \left({x}\right)\left({tan}^{\mathrm{2}} \left({x}\right)−\frac{\mathrm{2}}{\mathrm{5}}\right)+{C} \\ $$
Commented by tawa last updated on 25/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
