Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 107835 by PNL last updated on 12/Aug/20

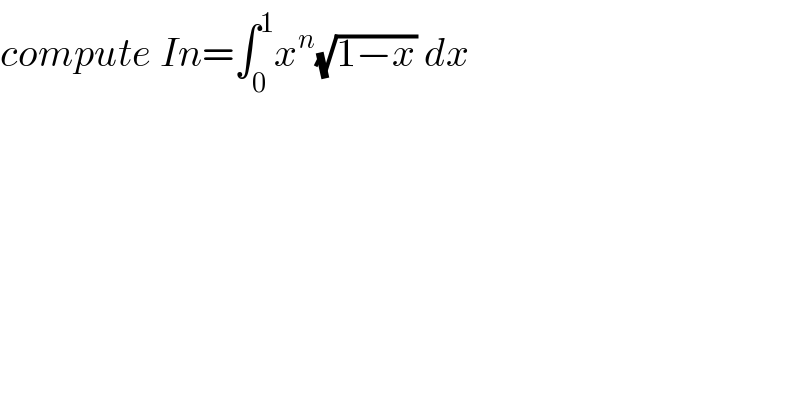
compute In=∫_0 ^1 x^n (√(1−x)) dx

$${compute}\:{In}=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \sqrt{\mathrm{1}−{x}}\:{dx} \\ $$

Answered by hgrocks last updated on 12/Aug/20

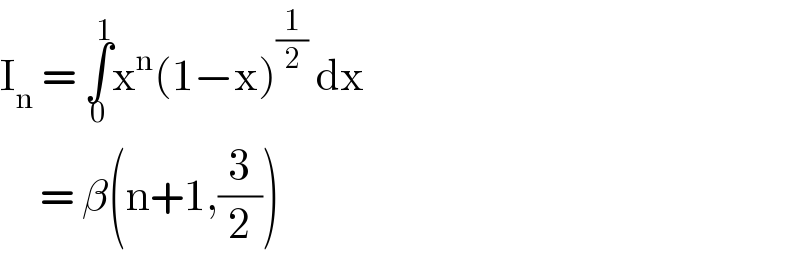
I_n = ∫_0 ^1 x^n (1−x)^(1/2) dx = β(n+1,(3/2))

$$\mathrm{I}_{\mathrm{n}} \:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\mathrm{x}^{\mathrm{n}} \left(\mathrm{1}−\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{dx} \\ $$$$\:\:\:\:\:=\:\beta\left(\mathrm{n}+\mathrm{1},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$

Answered by mathmax by abdo last updated on 12/Aug/20

I_n =∫_0 ^1 x^n (√(1−x))dx we do the changement x =sin^2 t ⇒ I_n =∫_0 ^(π/2) sin^(2n) t cost (2sint)cost dt =2∫_0 ^(π/2) cos^2 t sin^(2n+1) t dt we know 2∫_0 ^(π/2) cos^(2p−1) x sin^(2q−1) x dx =B(p,q) =((Γ(p).Γ(q))/(Γ(p+q))) 2p−1 =2 ⇒p=3 and 2q−1 =2n+1 ⇒2q=2n+2 ⇒q=n+1 ⇒ 2 ∫_0 ^(π/2) cos^2 t sin^(2n+1) t dt =2 ∫_0 ^(π/2) cos^(2((3/2))−1) sin^(2(n+1)−1) t dt =B((3/2),n+1) =((Γ((3/2))Γ(n+1))/(Γ((3/2)+n+1))) =((Γ((1/2)+1)n!)/((n+(3/2))Γ(n+(3/2)))) =(1/2)((Γ((1/2))n!)/((n+(3/2))(n+(1/2))Γ(n+(1/2))))

$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \sqrt{\mathrm{1}−\mathrm{x}}\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}\:=\mathrm{sin}^{\mathrm{2}} \mathrm{t}\:\Rightarrow \\ $$$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2n}} \mathrm{t}\:\mathrm{cost}\:\left(\mathrm{2sint}\right)\mathrm{cost}\:\mathrm{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\mathrm{cos}^{\mathrm{2}} \mathrm{t}\:\:\mathrm{sin}^{\mathrm{2n}+\mathrm{1}} \mathrm{t}\:\mathrm{dt}\:\:\mathrm{we}\:\mathrm{know} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2p}−\mathrm{1}} \mathrm{x}\:\mathrm{sin}^{\mathrm{2q}−\mathrm{1}} \mathrm{x}\:\mathrm{dx}\:=\mathrm{B}\left(\mathrm{p},\mathrm{q}\right)\:=\frac{\Gamma\left(\mathrm{p}\right).\Gamma\left(\mathrm{q}\right)}{\Gamma\left(\mathrm{p}+\mathrm{q}\right)} \\ $$$$\mathrm{2p}−\mathrm{1}\:=\mathrm{2}\:\Rightarrow\mathrm{p}=\mathrm{3}\:\mathrm{and}\:\mathrm{2q}−\mathrm{1}\:=\mathrm{2n}+\mathrm{1}\:\Rightarrow\mathrm{2q}=\mathrm{2n}+\mathrm{2}\:\Rightarrow\mathrm{q}=\mathrm{n}+\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{t}\:\mathrm{sin}^{\mathrm{2n}+\mathrm{1}} \mathrm{t}\:\mathrm{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\mathrm{1}} \:\mathrm{sin}^{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)−\mathrm{1}} \mathrm{t}\:\mathrm{dt} \\ $$$$=\mathrm{B}\left(\frac{\mathrm{3}}{\mathrm{2}},\mathrm{n}+\mathrm{1}\right)\:=\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left(\mathrm{n}+\mathrm{1}\right)}{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{n}+\mathrm{1}\right)}\:=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)\mathrm{n}!}{\left(\mathrm{n}+\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left(\mathrm{n}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{n}!}{\left(\mathrm{n}+\frac{\mathrm{3}}{\mathrm{2}}\right)\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$

Commented by PNL last updated on 13/Aug/20

$$ \\ $$

Commented by PNL last updated on 13/Aug/20

it′s a little difficult to understand

$${it}'{s}\:{a}\:{little}\:{difficult}\:{to}\:{understand} \\ $$

Commented by mathmax by abdo last updated on 13/Aug/20

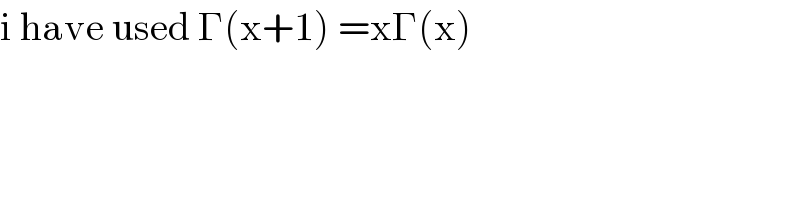
i have used Γ(x+1) =xΓ(x)

$$\mathrm{i}\:\mathrm{have}\:\mathrm{used}\:\Gamma\left(\mathrm{x}+\mathrm{1}\right)\:=\mathrm{x}\Gamma\left(\mathrm{x}\right) \\ $$

Commented by PNL last updated on 13/Aug/20

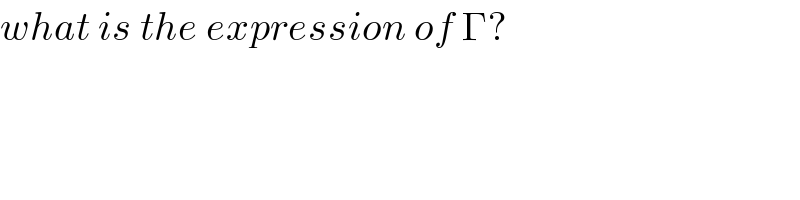
what is the expression of Γ?

$${what}\:{is}\:{the}\:{expression}\:{of}\:\Gamma? \\ $$

Commented by Aziztisffola last updated on 13/Aug/20

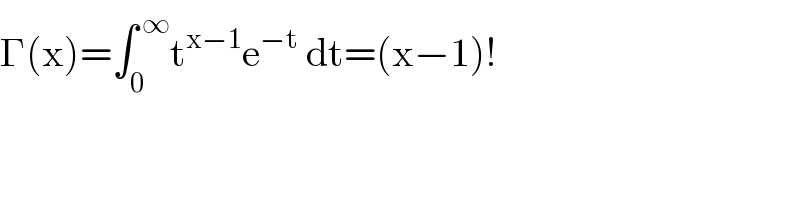
Γ(x)=∫_0 ^( ∞) t^(x−1) e^(−t) dt=(x−1)!

$$\Gamma\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\:\infty} \mathrm{t}^{\mathrm{x}−\mathrm{1}} \mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}=\left(\mathrm{x}−\mathrm{1}\right)! \\ $$

Commented by PNL last updated on 13/Aug/20

ok tanks. God bless you

$${ok}\:{tanks}.\:{God}\:{bless}\:{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com