
Question Number 155533 by mnjuly1970 last updated on 01/Oct/21
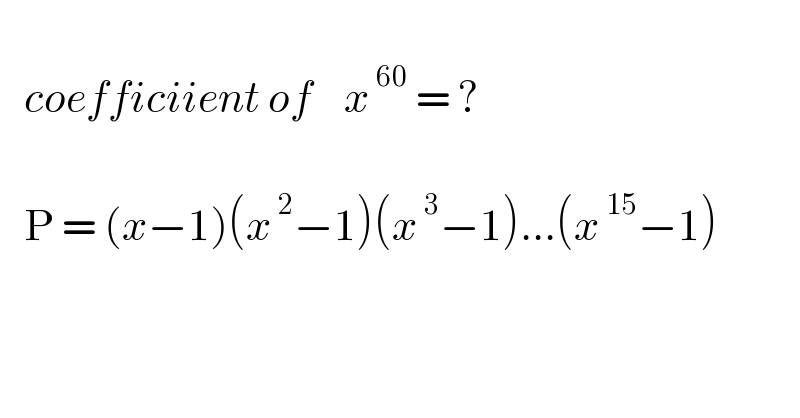
$$ \\ $$$$\:\:\:{coefficiient}\:{of}\:\:\:\:{x}^{\:\mathrm{60}} \:=\:? \\ $$$$ \\ $$$$\:\:\:\mathrm{P}\:=\:\left({x}−\mathrm{1}\right)\left({x}^{\:\mathrm{2}} −\mathrm{1}\right)\left({x}^{\:\mathrm{3}} −\mathrm{1}\right)...\left({x}^{\:\mathrm{15}} −\mathrm{1}\right) \\ $$$$ \\ $$
Answered by qaz last updated on 02/Oct/21
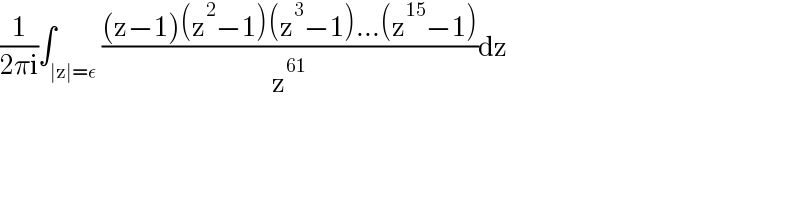
$$\frac{\mathrm{1}}{\mathrm{2}\pi\mathrm{i}}\int_{\mid\mathrm{z}\mid=\epsilon} \frac{\left(\mathrm{z}−\mathrm{1}\right)\left(\mathrm{z}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{z}^{\mathrm{3}} −\mathrm{1}\right)...\left(\mathrm{z}^{\mathrm{15}} −\mathrm{1}\right)}{\mathrm{z}^{\mathrm{61}} }\mathrm{dz} \\ $$
