
Question Number 115031 by bobhans last updated on 23/Sep/20
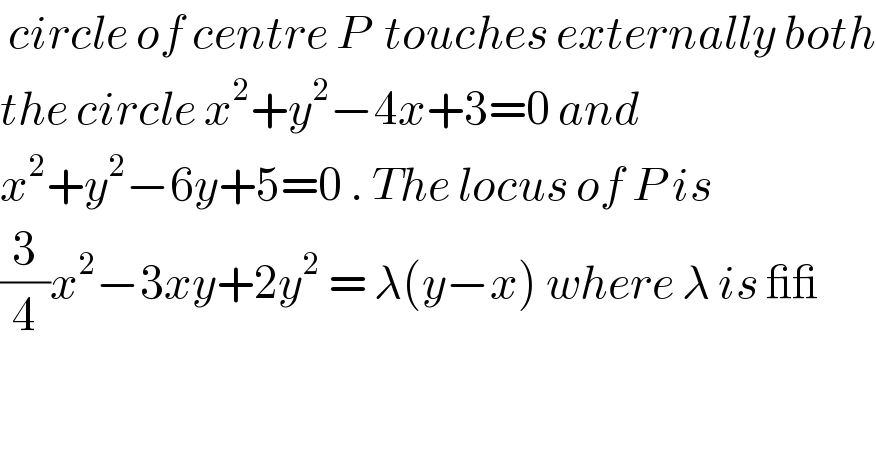
$$\:{circle}\:{of}\:{centre}\:{P}\:\:{touches}\:{externally}\:{both} \\ $$$${the}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}=\mathrm{0}\:{and}\: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{6}{y}+\mathrm{5}=\mathrm{0}\:.\:{The}\:{locus}\:{of}\:{P}\:{is} \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{2}} −\mathrm{3}{xy}+\mathrm{2}{y}^{\mathrm{2}} \:=\:\lambda\left({y}−{x}\right)\:{where}\:\lambda\:{is}\:\_\_ \\ $$
Answered by mr W last updated on 23/Sep/20
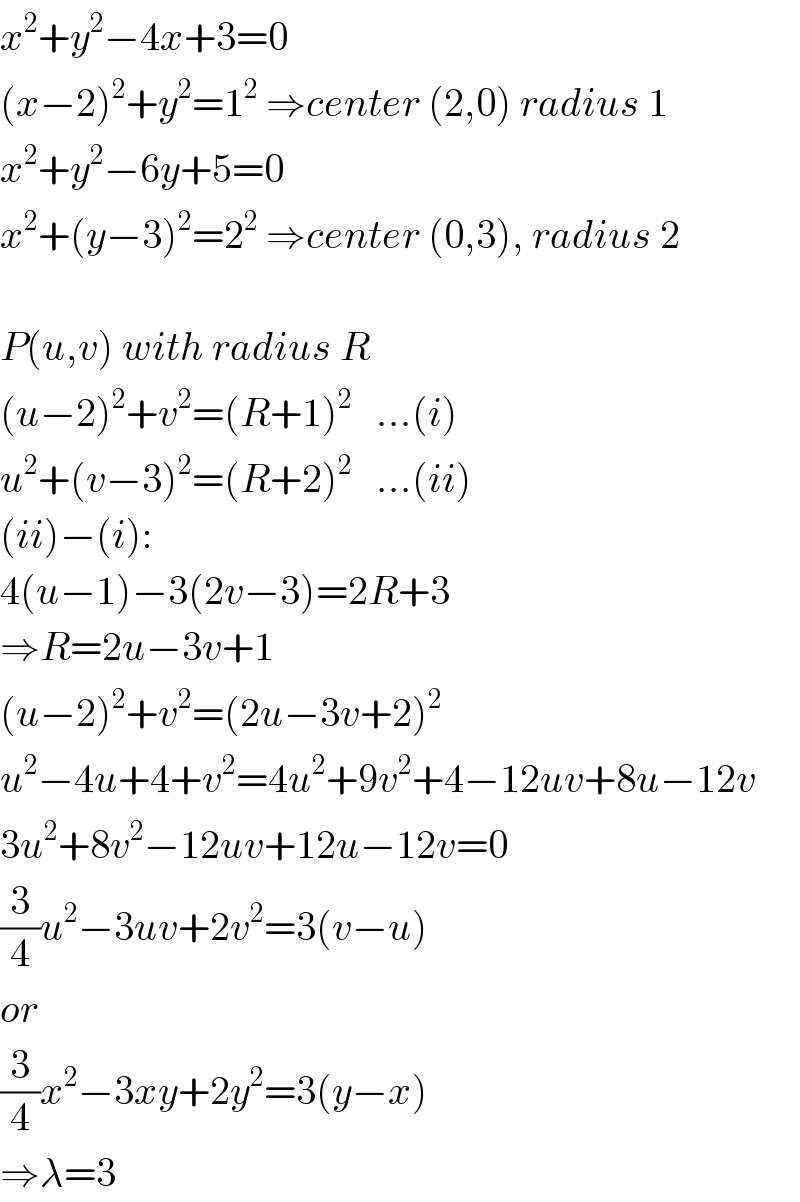
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}=\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} \:\Rightarrow{center}\:\left(\mathrm{2},\mathrm{0}\right)\:{radius}\:\mathrm{1} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{6}{y}+\mathrm{5}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\left({y}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} \:\Rightarrow{center}\:\left(\mathrm{0},\mathrm{3}\right),\:{radius}\:\mathrm{2} \\ $$$$ \\ $$$${P}\left({u},{v}\right)\:{with}\:{radius}\:{R} \\ $$$$\left({u}−\mathrm{2}\right)^{\mathrm{2}} +{v}^{\mathrm{2}} =\left({R}+\mathrm{1}\right)^{\mathrm{2}} \:\:\:...\left({i}\right) \\ $$$${u}^{\mathrm{2}} +\left({v}−\mathrm{3}\right)^{\mathrm{2}} =\left({R}+\mathrm{2}\right)^{\mathrm{2}} \:\:\:...\left({ii}\right) \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$$\mathrm{4}\left({u}−\mathrm{1}\right)−\mathrm{3}\left(\mathrm{2}{v}−\mathrm{3}\right)=\mathrm{2}{R}+\mathrm{3} \\ $$$$\Rightarrow{R}=\mathrm{2}{u}−\mathrm{3}{v}+\mathrm{1} \\ $$$$\left({u}−\mathrm{2}\right)^{\mathrm{2}} +{v}^{\mathrm{2}} =\left(\mathrm{2}{u}−\mathrm{3}{v}+\mathrm{2}\right)^{\mathrm{2}} \: \\ $$$${u}^{\mathrm{2}} −\mathrm{4}{u}+\mathrm{4}+{v}^{\mathrm{2}} =\mathrm{4}{u}^{\mathrm{2}} +\mathrm{9}{v}^{\mathrm{2}} +\mathrm{4}−\mathrm{12}{uv}+\mathrm{8}{u}−\mathrm{12}{v} \\ $$$$\mathrm{3}{u}^{\mathrm{2}} +\mathrm{8}{v}^{\mathrm{2}} −\mathrm{12}{uv}+\mathrm{12}{u}−\mathrm{12}{v}=\mathrm{0} \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}{u}^{\mathrm{2}} −\mathrm{3}{uv}+\mathrm{2}{v}^{\mathrm{2}} =\mathrm{3}\left({v}−{u}\right) \\ $$$${or} \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{2}} −\mathrm{3}{xy}+\mathrm{2}{y}^{\mathrm{2}} =\mathrm{3}\left({y}−{x}\right) \\ $$$$\Rightarrow\lambda=\mathrm{3} \\ $$
Commented by bobhans last updated on 23/Sep/20
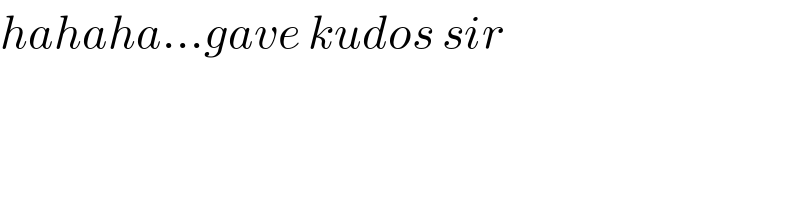
$${hahaha}...{gave}\:{kudos}\:{sir} \\ $$
Commented by bemath last updated on 23/Sep/20
Commented by bemath last updated on 23/Sep/20
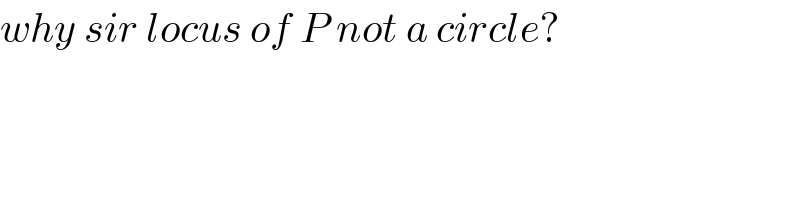
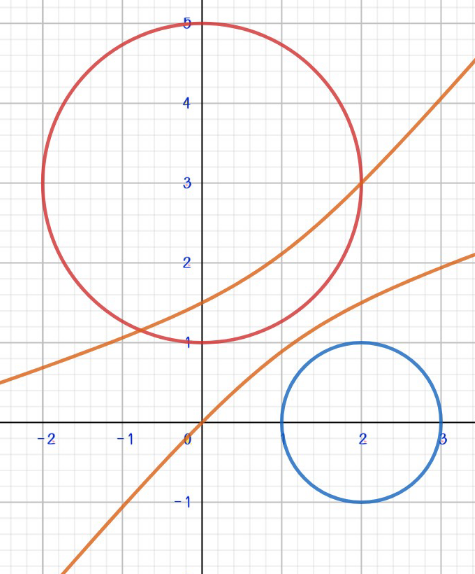
$${why}\:{sir}\:{locus}\:{of}\:{P}\:{not}\:{a}\:{circle}? \\ $$
Commented by mr W last updated on 23/Sep/20
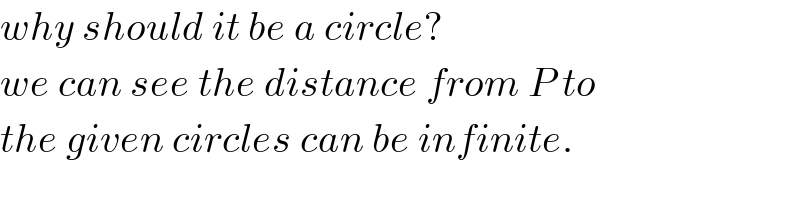
$${why}\:{should}\:{it}\:{be}\:{a}\:{circle}? \\ $$$${we}\:{can}\:{see}\:{the}\:{distance}\:{from}\:{P}\:{to} \\ $$$${the}\:{given}\:{circles}\:{can}\:{be}\:{infinite}. \\ $$
Commented by mr W last updated on 23/Sep/20

$${in}\:{fact}\:{it}\:{is}\:{clear}\:{that}\:{the}\:{locus}\:{is} \\ $$$${a}\:{hyperbola}.\:{just}\:{have}\:{a}\:{look}\:{at}\:{the} \\ $$$${definition}\:{of}\:{hyperbola}. \\ $$
Commented by bemath last updated on 23/Sep/20
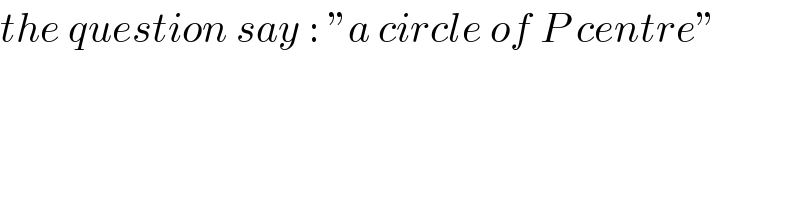
$${the}\:{question}\:{say}\::\:''{a}\:{circle}\:{of}\:{P}\:{centre}'' \\ $$
Commented by mr W last updated on 23/Sep/20

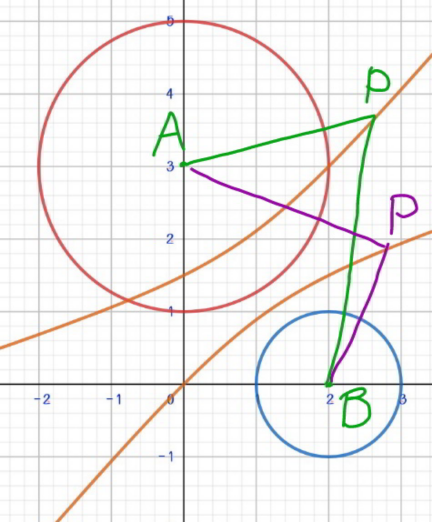
$${P}\:{is}\:{the}\:{center}\:{of}\:{a}\:{circle}\:{which} \\ $$$${tangents}\:{two}\:{given}\:{circles}.\:{but}\:{the} \\ $$$${locus}\:{of}\:{P}\:{is}\:{not}\:{a}\:{circle}!\:{say}\:{the}\:{two} \\ $$$${given}\:{circles}\:{are} \\ $$$${circle}\:\mathrm{1}\:{with}\:{center}\:{A}\:{and}\:{radius}\:{r}_{{A}} \\ $$$${circle}\:\mathrm{2}\:{with}\:{center}\:{B}\:{and}\:{radius}\:{r}_{{B}} \\ $$$${the}\:{circle}\:{with}\:{center}\:{P}\:{has}\:{radius}\:{R}. \\ $$$${we}\:{have} \\ $$$${PA}={r}_{{A}} +{R} \\ $$$${PB}={r}_{{B}} +{R} \\ $$$${PA}−{PB}={r}_{{A}} −{r}_{{B}} ={constant} \\ $$$${the}\:{locus}\:{of}\:{a}\:{point}\:{P},\:{whose}\: \\ $$$${difference}\:{distance}\:{to}\:{two}\:{given} \\ $$$${points}\:{A}\:{and}\:{B}\:{is}\:{constant},\:{is}\:{a} \\ $$$${hyperbola}. \\ $$
Commented by mr W last updated on 23/Sep/20
Commented by bemath last updated on 23/Sep/20
$${ooo}\:{i}\:{understood}\:{sir}.\:{gave}\:{kudos} \\ $$$${sir} \\ $$
Commented by otchereabdullai@gmail.com last updated on 24/Sep/20
$$\mathrm{more}\:\:\mathrm{blessing}\:\mathrm{prof} \\ $$
Commented by mr W last updated on 24/Sep/20

$${thanks}! \\ $$
