
Question Number 131286 by mnjuly1970 last updated on 03/Feb/21
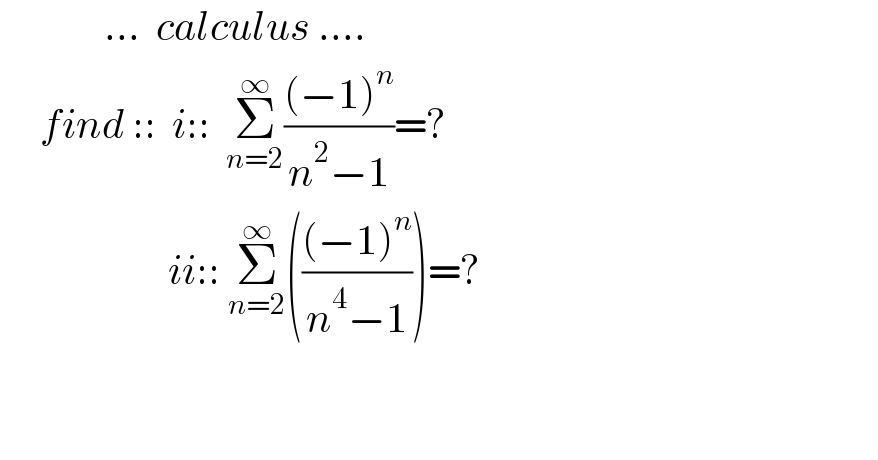
$$\:\:\:\:\:\:\:\:\:\:\:\:\:...\:\:{calculus}\:.... \\ $$$$\:\:\:\:\:{find}\:::\:\:{i}::\:\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} −\mathrm{1}}=? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{ii}::\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{4}} −\mathrm{1}}\right)=? \\ $$$$\:\:\:\: \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 03/Feb/21
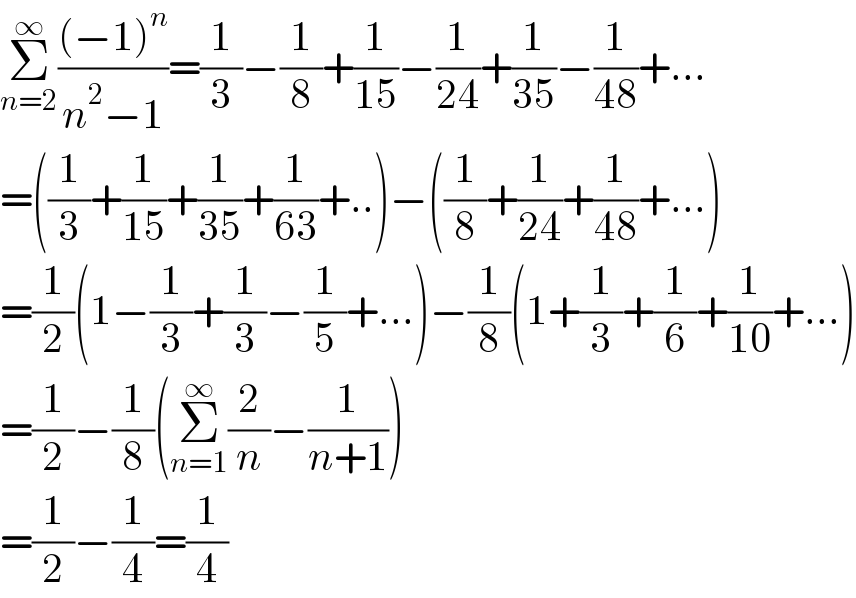
$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{15}}−\frac{\mathrm{1}}{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{35}}−\frac{\mathrm{1}}{\mathrm{48}}+... \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{15}}+\frac{\mathrm{1}}{\mathrm{35}}+\frac{\mathrm{1}}{\mathrm{63}}+..\right)−\left(\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{48}}+...\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}+...\right)−\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{10}}+...\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 03/Feb/21

$${thanks}\:\:{alot}\:{mr}\:{payan} \\ $$
Answered by Olaf last updated on 03/Feb/21
![S_1 = Σ_(n=2) ^∞ (((−1)^n )/(n^2 −1)) S_1 = Σ_(n=2) ^∞ (((−1)^n )/((n−1)(n+1))) S_1 = (1/2)[Σ_(n=2) ^∞ (((−1)^n )/(n−1))−Σ_(n=2) ^∞ (((−1)^n )/(n+1))] S_1 = (1/2)[Σ_(n=1) ^∞ (((−1)^(n+1) )/n)−Σ_(n=3) ^∞ (((−1)^(n−1) )/n)] S_1 = (1/2)[−Σ_(n=1) ^∞ (((−1)^n )/n)+Σ_(n=3) ^∞ (((−1)^n )/n)] S_1 = (1/2)[1−(1/2)] = (1/4) S_2 = Σ_(n=2) ^∞ (((−1)^n )/(n^4 −1)) S_2 = Σ_(n=2) ^∞ (((−1)^n )/((n^2 −1)(n^2 +1))) S_2 = (1/2)[Σ_(n=2) ^∞ (((−1)^n )/(n^2 −1))−Σ_(n=2) ^∞ (((−1)^n )/(n^2 +1))] S_2 = (1/2)[S_1 −Σ_(n=2) ^∞ (((−1)^n )/(n^2 +1))] S_2 = (1/8)−(1/2){−(i/4)[−Ψ(1−(i/2))+Ψ(1+(i/2)) +Ψ((3/2)−(i/2))−Ψ((3/2)+(i/2))]} S_2 = (1/8)−(1/2){(π/(2sinhπ))} S_2 = (1/8)−(π/(4sinhπ))](Q131292.png)
$$\mathrm{S}_{\mathrm{1}} \:=\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{S}_{\mathrm{1}} \:=\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)} \\ $$$$\mathrm{S}_{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}−\mathrm{1}}−\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\right] \\ $$$$\mathrm{S}_{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}}−\underset{{n}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\right] \\ $$$$\mathrm{S}_{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}+\underset{{n}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\right] \\ $$$$\mathrm{S}_{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right]\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$$$\mathrm{S}_{\mathrm{2}} \:=\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{4}} −\mathrm{1}} \\ $$$$\mathrm{S}_{\mathrm{2}} \:=\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}^{\mathrm{2}} −\mathrm{1}\right)\left({n}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\mathrm{S}_{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} −\mathrm{1}}−\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$\mathrm{S}_{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{S}_{\mathrm{1}} −\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$\mathrm{S}_{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\left\{−\frac{{i}}{\mathrm{4}}\left[−\Psi\left(\mathrm{1}−\frac{{i}}{\mathrm{2}}\right)+\Psi\left(\mathrm{1}+\frac{{i}}{\mathrm{2}}\right)\right.\right. \\ $$$$\left.+\left.\Psi\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{{i}}{\mathrm{2}}\right)−\Psi\left(\frac{\mathrm{3}}{\mathrm{2}}+\frac{{i}}{\mathrm{2}}\right)\right]\right\} \\ $$$$\mathrm{S}_{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\pi}{\mathrm{2sinh}\pi}\right\} \\ $$$$\mathrm{S}_{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{8}}−\frac{\pi}{\mathrm{4sinh}\pi} \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 03/Feb/21

$${mercey}\:{and}\:{grateful}\:{mr}\:{olaf}... \\ $$
