Question Number 140671 by mnjuly1970 last updated on 11/May/21
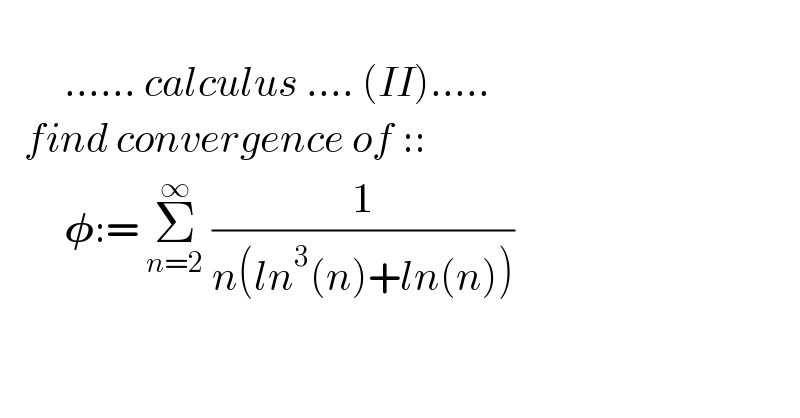
$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:......\:{calculus}\:....\:\left({II}\right)..... \\ $$$$\:\:\:{find}\:{convergence}\:{of}\::: \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{\phi}:=\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}\left({ln}^{\mathrm{3}} \left({n}\right)+{ln}\left({n}\right)\right)}\: \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 11/May/21
![Ď(x)=(1/(x(log^3 x +logx))) (x>2) âĎ^Ⲡ(x)=â((log^3 x +logx +x(((3log^2 x)/x)+(1/x)))/(x^2 (log^3 x+logx)^2 )) =â((log^3 x+logx+3log^2 x+1)/(x^2 (log^3 x+logx)^2 ))<0 âĎ is decreazing on[2,+â[ â so ÎŁ(...) and âŤ_e ^â (dt/(t(log^3 t +logt))) are the same nature of convergence ÎŚ=âŤ_e ^â (dt/(t(log^3 t +logt))) =_(logt=x) âŤ_1 ^â ((e^x dx)/(e^x (x^3 +x))) =âŤ_1 ^â (dx/(x^3 +x)) =âŤ_1 ^â (dx/(x(x^2 +1))) =âŤ_1 ^â ((1/x)â(x/(1+x^2 )))dx =[lnâŁ(x/( (â(1+x^2 ))))âŁ]_1 ^â <+â âÎŚ converges âÎŁ u_n converge...](Q140707.png)
$$\varphi\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{log}^{\mathrm{3}} \mathrm{x}\:+\mathrm{logx}\right)}\:\:\left(\mathrm{x}>\mathrm{2}\right)\:\Rightarrow\varphi^{'} \left(\mathrm{x}\right)=â\frac{\mathrm{log}^{\mathrm{3}} \mathrm{x}\:+\mathrm{logx}\:+\mathrm{x}\left(\frac{\mathrm{3log}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}}\right)}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{log}^{\mathrm{3}} \mathrm{x}+\mathrm{logx}\right)^{\mathrm{2}} } \\ $$$$=â\frac{\mathrm{log}^{\mathrm{3}} \mathrm{x}+\mathrm{logx}+\mathrm{3log}^{\mathrm{2}} \mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{log}^{\mathrm{3}} \mathrm{x}+\mathrm{logx}\right)^{\mathrm{2}} }<\mathrm{0}\:\Rightarrow\varphi\:\mathrm{is}\:\mathrm{decreazing}\:\mathrm{on}\left[\mathrm{2},+\infty\left[\:\Rightarrow\right.\right. \\ $$$$\mathrm{so}\:\Sigma\left(...\right)\:\mathrm{and}\:\int_{\mathrm{e}} ^{\infty} \:\:\:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{log}^{\mathrm{3}} \mathrm{t}\:+\mathrm{logt}\right)}\:\mathrm{are}\:\mathrm{the}\:\mathrm{same}\:\mathrm{nature}\:\mathrm{of}\:\mathrm{convergence} \\ $$$$\Phi=\int_{\mathrm{e}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{log}^{\mathrm{3}} \mathrm{t}\:+\mathrm{logt}\right)}\:=_{\mathrm{logt}=\mathrm{x}} \:\:\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{x}} \mathrm{dx}}{\mathrm{e}^{\mathrm{x}} \left(\mathrm{x}^{\mathrm{3}} \:+\mathrm{x}\right)} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} \:+\mathrm{x}}\:=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\int_{\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{x}}â\frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx} \\ $$$$=\left[\mathrm{ln}\mid\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\mid\right]_{\mathrm{1}} ^{\infty} <+\infty\:\Rightarrow\Phi\:\mathrm{converges}\:\Rightarrow\Sigma\:\mathrm{u}_{\mathrm{n}} \:\mathrm{converge}... \\ $$
Commented by mnjuly1970 last updated on 12/May/21
$$\:{great}\:{sir}\:{max}\:... \\ $$