Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 214144 by a.lgnaoui last updated on 29/Nov/24

calculer n

$$\mathrm{calculer}\:\:\mathrm{n}\:\:\:\: \\ $$

Commented by a.lgnaoui last updated on 29/Nov/24

Commented by issac last updated on 29/Nov/24

n..?

$${n}..? \\ $$

Commented by som(math1967) last updated on 29/Nov/24

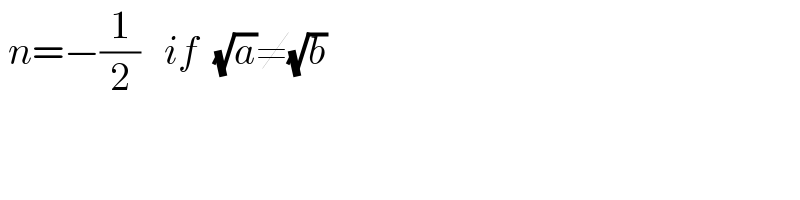
n=−(1/2) if (√a)≠(√b)

$$\:{n}=−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:{if}\:\:\sqrt{{a}}\neq\sqrt{{b}} \\ $$

Commented by issac last updated on 29/Nov/24

huh...? why...? why n=−(1/2)

$$\mathrm{huh}...?\:\mathrm{why}...? \\ $$$$\mathrm{why}\:{n}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by som(math1967) last updated on 29/Nov/24

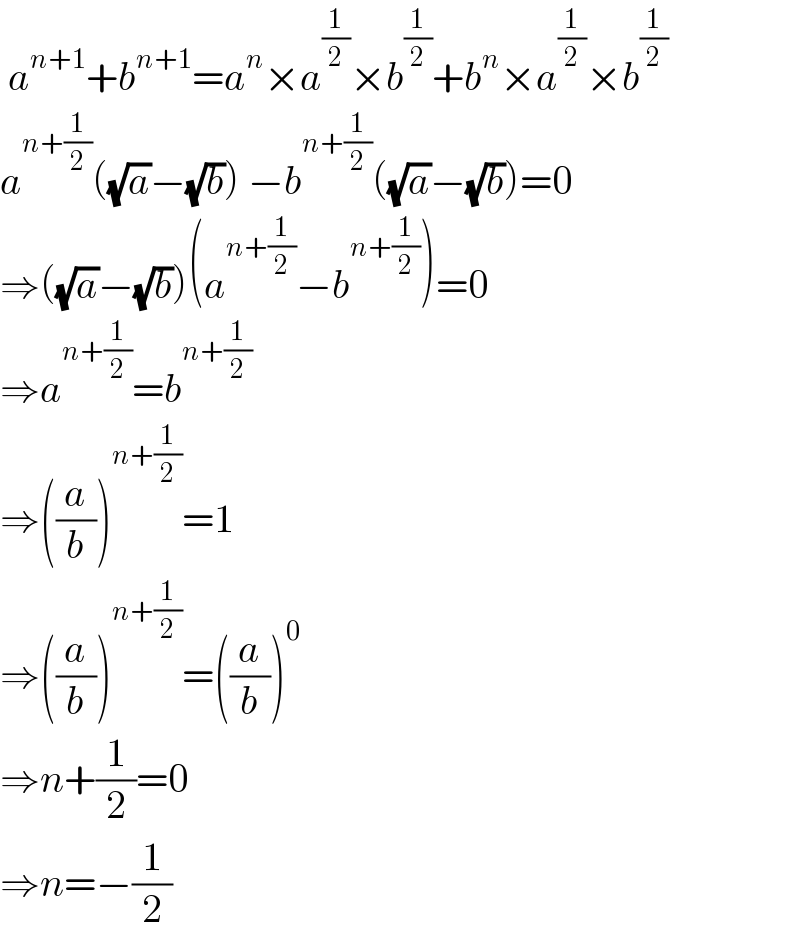
a^(n+1) +b^(n+1) =a^n ×a^(1/2) ×b^(1/2) +b^n ×a^(1/2) ×b^(1/2) a^(n+(1/2)) ((√a)−(√b)) −b^(n+(1/2)) ((√a)−(√b))=0 ⇒((√a)−(√b))(a^(n+(1/2)) −b^(n+(1/2)) )=0 ⇒a^(n+(1/2)) =b^(n+(1/2)) ⇒((a/b))^(n+(1/2)) =1 ⇒((a/b))^(n+(1/2)) =((a/b))^0 ⇒n+(1/2)=0 ⇒n=−(1/2)

$$\:{a}^{{n}+\mathrm{1}} +{b}^{{n}+\mathrm{1}} ={a}^{{n}} ×{a}^{\frac{\mathrm{1}}{\mathrm{2}}} ×{b}^{\frac{\mathrm{1}}{\mathrm{2}}} +{b}^{{n}} ×{a}^{\frac{\mathrm{1}}{\mathrm{2}}} ×{b}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \left(\sqrt{{a}}−\sqrt{{b}}\right)\:−{b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \left(\sqrt{{a}}−\sqrt{{b}}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\sqrt{{a}}−\sqrt{{b}}\right)\left({a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} −{b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \right)=\mathrm{0} \\ $$$$\Rightarrow{a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} ={b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\Rightarrow\left(\frac{{a}}{{b}}\right)^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{1} \\ $$$$\Rightarrow\left(\frac{{a}}{{b}}\right)^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} =\left(\frac{{a}}{{b}}\right)^{\mathrm{0}} \\ $$$$\Rightarrow{n}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow{n}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by issac last updated on 29/Nov/24

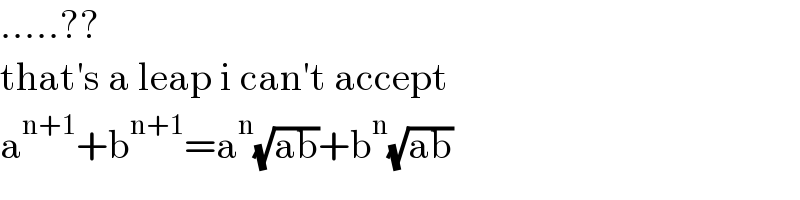
.....?? that′s a leap i can′t accept a^(n+1) +b^(n+1) =a^n (√(ab))+b^n (√(ab))

$$.....?? \\ $$$$\mathrm{that}'\mathrm{s}\:\mathrm{a}\:\mathrm{leap}\:\mathrm{i}\:\mathrm{can}'\mathrm{t}\:\mathrm{accept} \\ $$$$\mathrm{a}^{\mathrm{n}+\mathrm{1}} +\mathrm{b}^{\mathrm{n}+\mathrm{1}} =\mathrm{a}^{\mathrm{n}} \sqrt{\mathrm{ab}}+\mathrm{b}^{\mathrm{n}} \sqrt{\mathrm{ab}} \\ $$

Commented by mr W last updated on 29/Nov/24

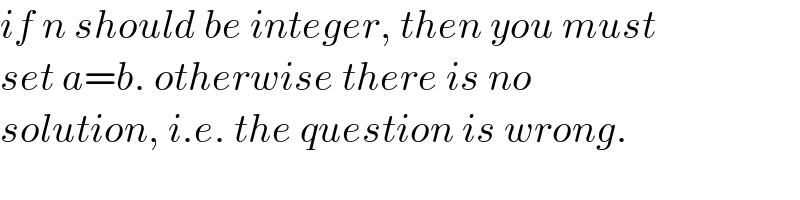
if n should be integer, then you must set a=b. otherwise there is no solution, i.e. the question is wrong.

$${if}\:{n}\:{should}\:{be}\:{integer},\:{then}\:{you}\:{must} \\ $$$${set}\:{a}={b}.\:{otherwise}\:{there}\:{is}\:{no} \\ $$$${solution},\:{i}.{e}.\:{the}\:{question}\:{is}\:{wrong}. \\ $$

Commented by laphop last updated on 01/Dec/24

I really like it, I solved it for a^n+b^m.

Answered by mr W last updated on 29/Nov/24

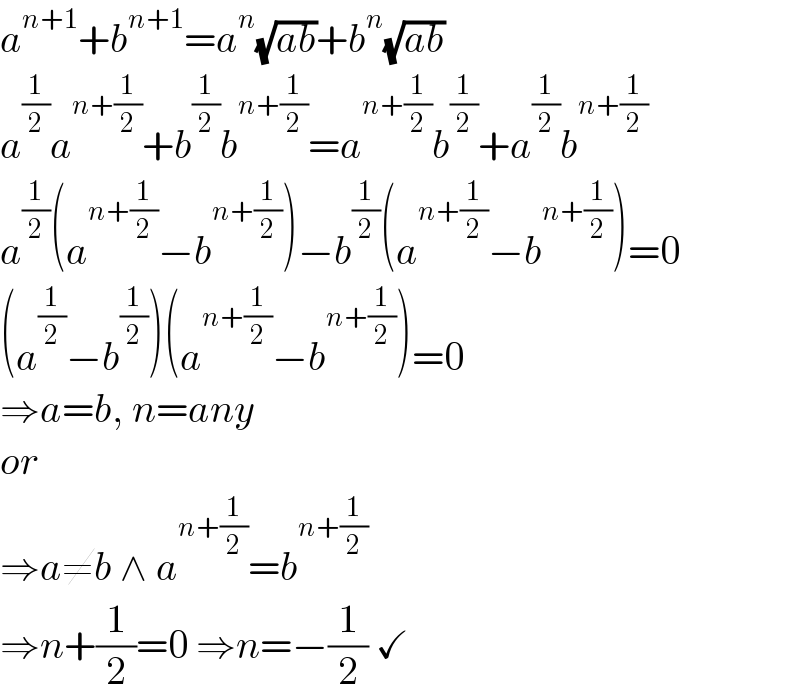
a^(n+1) +b^(n+1) =a^n (√(ab))+b^n (√(ab)) a^(1/2) a^(n+(1/2)) +b^(1/2) b^(n+(1/2)) =a^(n+(1/2)) b^(1/2) +a^(1/2) b^(n+(1/2)) a^(1/2) (a^(n+(1/2)) −b^(n+(1/2)) )−b^(1/2) (a^(n+(1/2)) −b^(n+(1/2)) )=0 (a^(1/2) −b^(1/2) )(a^(n+(1/2)) −b^(n+(1/2)) )=0 ⇒a=b, n=any or ⇒a≠b ∧ a^(n+(1/2)) =b^(n+(1/2)) ⇒n+(1/2)=0 ⇒n=−(1/2) ✓

$${a}^{{n}+\mathrm{1}} +{b}^{{n}+\mathrm{1}} ={a}^{{n}} \sqrt{{ab}}+{b}^{{n}} \sqrt{{ab}} \\ $$$${a}^{\frac{\mathrm{1}}{\mathrm{2}}} {a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} +{b}^{\frac{\mathrm{1}}{\mathrm{2}}} {b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} ={a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} {b}^{\frac{\mathrm{1}}{\mathrm{2}}} +{a}^{\frac{\mathrm{1}}{\mathrm{2}}} {b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${a}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} −{b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \right)−{b}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} −{b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \right)=\mathrm{0} \\ $$$$\left({a}^{\frac{\mathrm{1}}{\mathrm{2}}} −{b}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)\left({a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} −{b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \right)=\mathrm{0} \\ $$$$\Rightarrow{a}={b},\:{n}={any} \\ $$$${or} \\ $$$$\Rightarrow{a}\neq{b}\:\wedge\:{a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} ={b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \: \\ $$$$\Rightarrow{n}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0}\:\Rightarrow{n}=−\frac{\mathrm{1}}{\mathrm{2}}\:\checkmark \\ $$

Commented by a.lgnaoui last updated on 29/Nov/24

thanks

$$\mathrm{thanks} \\ $$

Commented by issac last updated on 29/Nov/24

hmmm....... good solution Bro

$$\mathrm{hmmm}.......\:\mathrm{good}\:\mathrm{solution}\:\mathrm{Bro} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com