Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 77897 by mathmax by abdo last updated on 11/Jan/20

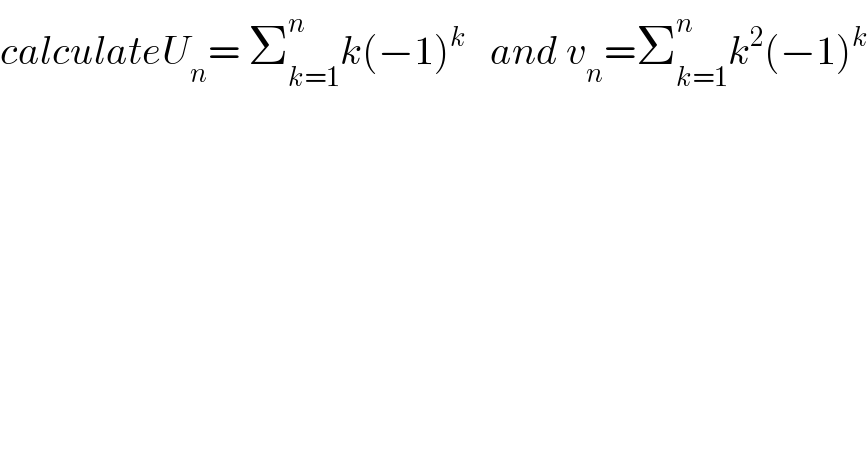
calculateU_n = Σ_(k=1) ^n k(−1)^k and v_n =Σ_(k=1) ^n k^2 (−1)^k

$${calculateU}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} {k}\left(−\mathrm{1}\right)^{{k}} \:\:\:{and}\:{v}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} {k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} \\ $$

Commented by abdomathmax last updated on 12/Jan/20

for v_n =Σ_(k=1) ^n k^2 (−1)^k we consider again p(x)=Σ_(k=0) ^n x^k we have xp^′ (x)=Σ_(k=1) ^n kx^k ⇒ p^′ (x)+xp^(′′) (x)=Σ_(k=1) ^n k^2 x^(k−1) ⇒ xp^′ (x)+x^2 p^((2)) (x) =Σ_(k=1) ^n k^2 x^k ⇒ Σ_(k=1) ^n k^2 (−1)^k =−p^′ (−1)+p^((2)) (−1) we have p^′ (x)=((nx^(n+1) −(n+1)x^n +1)/((x−1)^2 )) ⇒ p^((2)) (x)=(((n(n+1)x^n −n(n+1)x^(n−1) )(x−1)^2 −2(x−1)(nx^(n+1) −(n+1)x^n +1))/((x−1)^4 )) =((n(n+1)(x^n −x^(n−1) )(x−1)−2(nx^(n+1) −(n+1)x^n +1))/((x−1)^3 )) =((n(n+1)(x^(n+1) −x^n −x^n +x^(n−1) )−2nx^(n+1) +2(n+1)x^n −2)/((x−1)^3 )) =((n(n+1)x^(n+1) −2n(n+1)x^n +n(n+1)x^(n−1) −2nx^(n+1) +2(n+1)x^n −2)/((x−1)^3 )) =(((n^2 −n)x^(n+1) +(−2n^2 −2n+2n+2)x^n +n(n+1)x^(n−1) −2)/((x−1)^3 )) =(((n^2 −n)x^(n+1) +(−2n^2 +2)x^n +n(n+1)x^(n−1) −2)/((x−1)^3 )) ⇒p^((2)) (−1) =(((n−n^2 )(−1)^n +(2−2n^2 )(−1)^n −(n^2 +n)(−1)^n −2)/(−8)) =(((n−n^2 +2−2n^2 −n^2 −n)(−1)^n −2)/(−8)) =(((2−4n^2 )(−1)^n −2)/(−8)) =(((2n^2 −1)(−1)^n +1)/4) ⇒v_n =p^((2)) (−1)−p^′ (−1) =(((2n^2 −1)(−1)^n +1)/4)−((1−(2n+1)(−1)^n )/4) =(((2n^2 −1+2n+1)(−1)^n )/4) =(((n^2 +n)(−1)^n )/2)

$${for}\:{v}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} {k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} \:\:{we}\:{consider}\:{again} \\ $$$${p}\left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:{x}^{{k}} \:\:{we}\:{have}\:{xp}^{'} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} {kx}^{{k}} \:\Rightarrow \\ $$$${p}^{'} \left({x}\right)+{xp}^{''} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} {k}^{\mathrm{2}} {x}^{{k}−\mathrm{1}} \:\Rightarrow \\ $$$${xp}^{'} \left({x}\right)+{x}^{\mathrm{2}} {p}^{\left(\mathrm{2}\right)} \left({x}\right)\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}^{\mathrm{2}} {x}^{{k}} \:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} {k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} \:=−{p}^{'} \left(−\mathrm{1}\right)+{p}^{\left(\mathrm{2}\right)} \left(−\mathrm{1}\right) \\ $$$${we}\:{have}\:{p}^{'} \left({x}\right)=\frac{{nx}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${p}^{\left(\mathrm{2}\right)} \left({x}\right)=\frac{\left({n}\left({n}+\mathrm{1}\right){x}^{{n}} −{n}\left({n}+\mathrm{1}\right){x}^{{n}−\mathrm{1}} \right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left({x}−\mathrm{1}\right)\left({nx}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}} +\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left({x}^{{n}} −{x}^{{n}−\mathrm{1}} \right)\left({x}−\mathrm{1}\right)−\mathrm{2}\left({nx}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}} +\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left({x}^{{n}+\mathrm{1}} −{x}^{{n}} −{x}^{{n}} +{x}^{{n}−\mathrm{1}} \right)−\mathrm{2}{nx}^{{n}+\mathrm{1}} +\mathrm{2}\left({n}+\mathrm{1}\right){x}^{{n}} −\mathrm{2}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} −\mathrm{2}{n}\left({n}+\mathrm{1}\right){x}^{{n}} +{n}\left({n}+\mathrm{1}\right){x}^{{n}−\mathrm{1}} −\mathrm{2}{nx}^{{n}+\mathrm{1}} +\mathrm{2}\left({n}+\mathrm{1}\right){x}^{{n}} −\mathrm{2}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left({n}^{\mathrm{2}} −{n}\right){x}^{{n}+\mathrm{1}} +\left(−\mathrm{2}{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{2}{n}+\mathrm{2}\right){x}^{{n}} \:+{n}\left({n}+\mathrm{1}\right){x}^{{n}−\mathrm{1}} −\mathrm{2}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left({n}^{\mathrm{2}} −{n}\right){x}^{{n}+\mathrm{1}} \:+\left(−\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}\right){x}^{{n}} \:+{n}\left({n}+\mathrm{1}\right){x}^{{n}−\mathrm{1}} −\mathrm{2}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\Rightarrow{p}^{\left(\mathrm{2}\right)} \left(−\mathrm{1}\right)\:=\frac{\left({n}−{n}^{\mathrm{2}} \right)\left(−\mathrm{1}\right)^{{n}} +\left(\mathrm{2}−\mathrm{2}{n}^{\mathrm{2}} \right)\left(−\mathrm{1}\right)^{{n}} −\left({n}^{\mathrm{2}} +{n}\right)\left(−\mathrm{1}\right)^{{n}} −\mathrm{2}}{−\mathrm{8}} \\ $$$$=\frac{\left({n}−{n}^{\mathrm{2}} +\mathrm{2}−\mathrm{2}{n}^{\mathrm{2}} −{n}^{\mathrm{2}} −{n}\right)\left(−\mathrm{1}\right)^{{n}} −\mathrm{2}}{−\mathrm{8}} \\ $$$$=\frac{\left(\mathrm{2}−\mathrm{4}{n}^{\mathrm{2}} \right)\left(−\mathrm{1}\right)^{{n}} −\mathrm{2}}{−\mathrm{8}}\:=\frac{\left(\mathrm{2}{n}^{\mathrm{2}} −\mathrm{1}\right)\left(−\mathrm{1}\right)^{\boldsymbol{{n}}} \:+\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{v}_{{n}} ={p}^{\left(\mathrm{2}\right)} \left(−\mathrm{1}\right)−{p}^{'} \left(−\mathrm{1}\right) \\ $$$$=\frac{\left(\mathrm{2}{n}^{\mathrm{2}} −\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} +\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}−\left(\mathrm{2}{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}} \\ $$$$=\frac{\left(\mathrm{2}{n}^{\mathrm{2}} −\mathrm{1}+\mathrm{2}{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}}\:=\frac{\left({n}^{\mathrm{2}} +{n}\right)\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}} \\ $$

Commented by abdomathmax last updated on 12/Jan/20

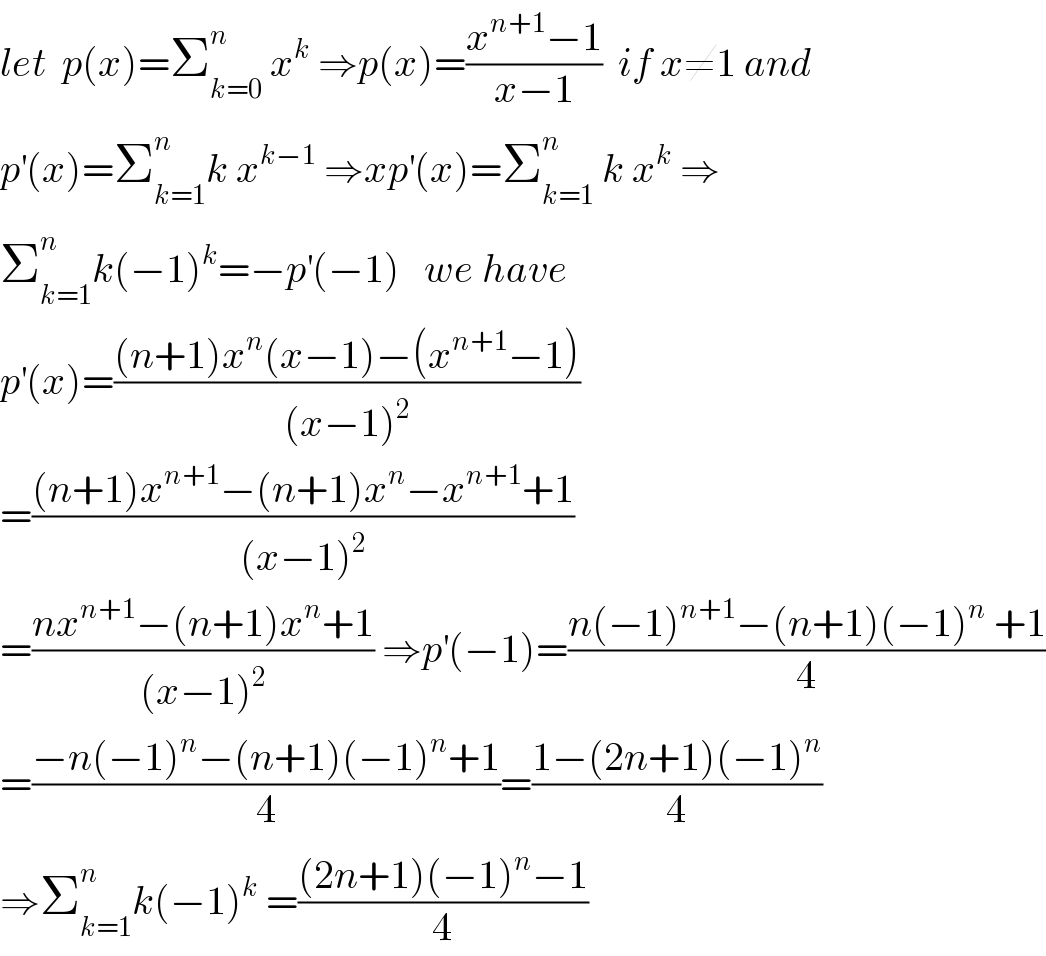
let p(x)=Σ_(k=0) ^n x^k ⇒p(x)=((x^(n+1) −1)/(x−1)) if x≠1 and p^′ (x)=Σ_(k=1) ^n k x^(k−1) ⇒xp^′ (x)=Σ_(k=1) ^n k x^k ⇒ Σ_(k=1) ^n k(−1)^k =−p^′ (−1) we have p^′ (x)=(((n+1)x^n (x−1)−(x^(n+1) −1))/((x−1)^2 )) =(((n+1)x^(n+1) −(n+1)x^n −x^(n+1) +1)/((x−1)^2 )) =((nx^(n+1) −(n+1)x^n +1)/((x−1)^2 )) ⇒p^′ (−1)=((n(−1)^(n+1) −(n+1)(−1)^n +1)/4) =((−n(−1)^n −(n+1)(−1)^n +1)/4)=((1−(2n+1)(−1)^n )/4) ⇒Σ_(k=1) ^n k(−1)^k =(((2n+1)(−1)^n −1)/4)

$${let}\:\:{p}\left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:{x}^{{k}} \:\Rightarrow{p}\left({x}\right)=\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\:\:{if}\:{x}\neq\mathrm{1}\:{and} \\ $$$${p}^{'} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} {k}\:{x}^{{k}−\mathrm{1}} \:\Rightarrow{xp}^{'} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:{x}^{{k}} \:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} {k}\left(−\mathrm{1}\right)^{{k}} =−{p}^{'} \left(−\mathrm{1}\right)\:\:\:{we}\:{have}\: \\ $$$${p}^{'} \left({x}\right)=\frac{\left({n}+\mathrm{1}\right){x}^{{n}} \left({x}−\mathrm{1}\right)−\left({x}^{{n}+\mathrm{1}} −\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}} −{x}^{{n}+\mathrm{1}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{{nx}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow{p}^{'} \left(−\mathrm{1}\right)=\frac{{n}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} \:+\mathrm{1}}{\mathrm{4}} \\ $$$$=\frac{−{n}\left(−\mathrm{1}\right)^{{n}} −\left({n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} +\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}−\left(\mathrm{2}{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}} \\ $$$$\Rightarrow\sum_{{k}=\mathrm{1}} ^{{n}} {k}\left(−\mathrm{1}\right)^{{k}} \:=\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}}{\mathrm{4}} \\ $$

Commented by abdomathmax last updated on 12/Jan/20

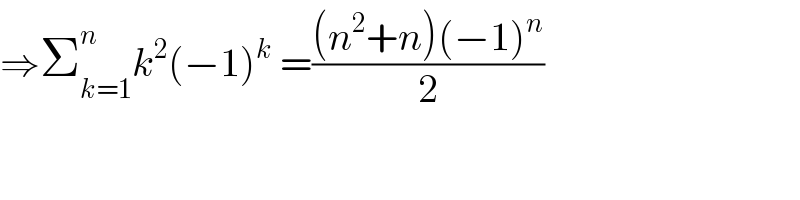
⇒Σ_(k=1) ^n k^2 (−1)^k =(((n^2 +n)(−1)^n )/2)

$$\Rightarrow\sum_{{k}=\mathrm{1}} ^{{n}} {k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} \:=\frac{\left({n}^{\mathrm{2}} +{n}\right)\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}} \\ $$

Commented by john santu last updated on 12/Jan/20

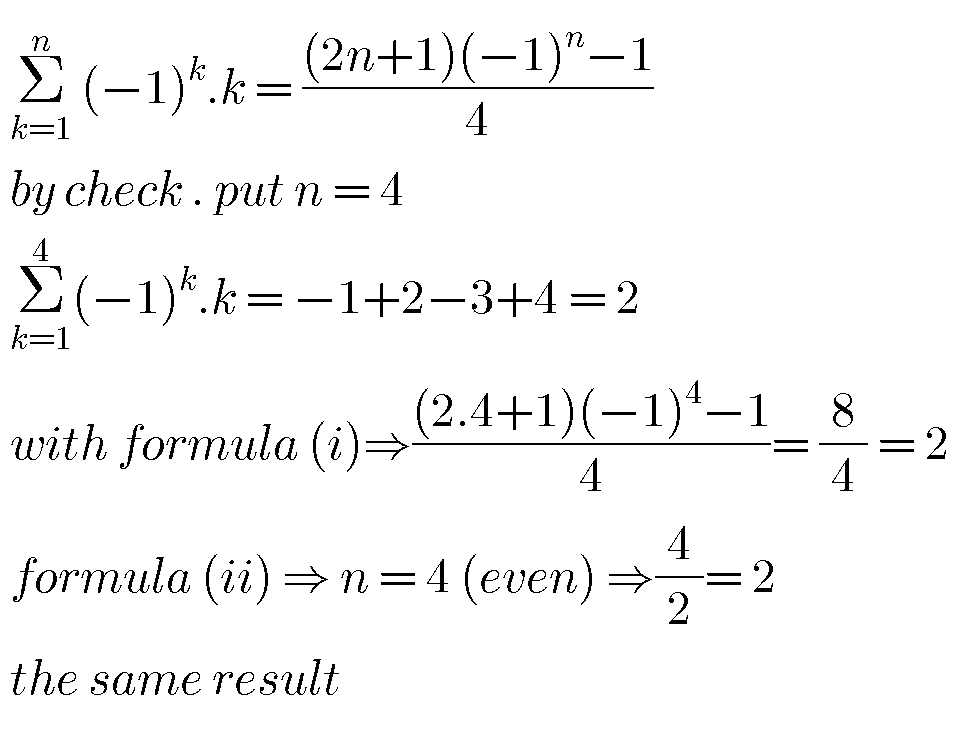
Commented by john santu last updated on 12/Jan/20

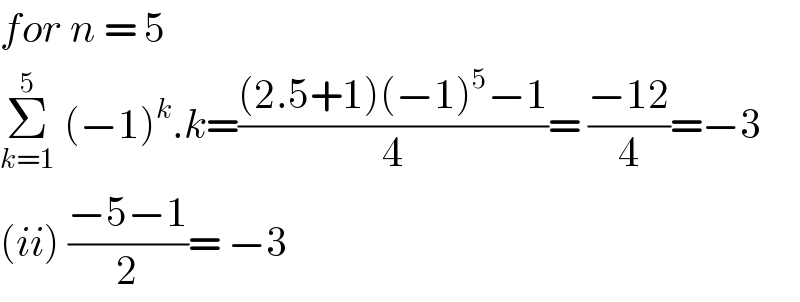
for n = 5 Σ_(k=1) ^5 (−1)^k .k=(((2.5+1)(−1)^5 −1)/4)= ((−12)/4)=−3 (ii) ((−5−1)/2)= −3

$${for}\:{n}\:=\:\mathrm{5}\: \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{5}} {\sum}}\:\left(−\mathrm{1}\right)^{{k}} .{k}=\frac{\left(\mathrm{2}.\mathrm{5}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{5}} −\mathrm{1}}{\mathrm{4}}=\:\frac{−\mathrm{12}}{\mathrm{4}}=−\mathrm{3} \\ $$$$\left({ii}\right)\:\frac{−\mathrm{5}−\mathrm{1}}{\mathrm{2}}=\:−\mathrm{3} \\ $$

Answered by jagoll last updated on 12/Jan/20

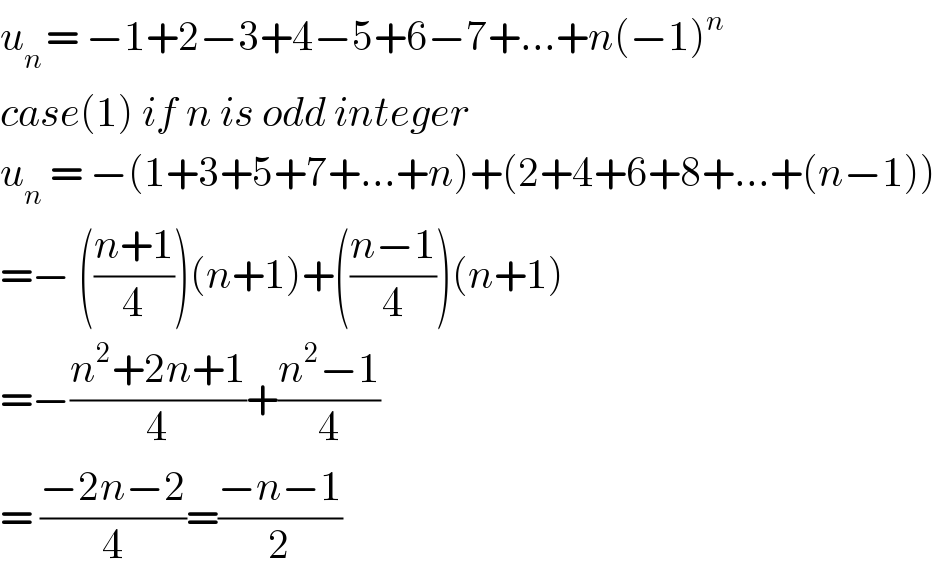
u_(n ) = −1+2−3+4−5+6−7+...+n(−1)^n case(1) if n is odd integer u_n = −(1+3+5+7+...+n)+(2+4+6+8+...+(n−1)) =− (((n+1)/4))(n+1)+(((n−1)/4))(n+1) =−((n^2 +2n+1)/4)+((n^2 −1)/4) = ((−2n−2)/4)=((−n−1)/2)

$${u}_{{n}\:} =\:−\mathrm{1}+\mathrm{2}−\mathrm{3}+\mathrm{4}−\mathrm{5}+\mathrm{6}−\mathrm{7}+...+{n}\left(−\mathrm{1}\right)^{{n}} \\ $$$${case}\left(\mathrm{1}\right)\:{if}\:{n}\:{is}\:{odd}\:{integer} \\ $$$${u}_{{n}} \:=\:−\left(\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}+...+{n}\right)+\left(\mathrm{2}+\mathrm{4}+\mathrm{6}+\mathrm{8}+...+\left({n}−\mathrm{1}\right)\right) \\ $$$$=−\:\left(\frac{{n}+\mathrm{1}}{\mathrm{4}}\right)\left({n}+\mathrm{1}\right)+\left(\frac{{n}−\mathrm{1}}{\mathrm{4}}\right)\left({n}+\mathrm{1}\right) \\ $$$$=−\frac{{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}}{\mathrm{4}}+\frac{{n}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}} \\ $$$$=\:\frac{−\mathrm{2}{n}−\mathrm{2}}{\mathrm{4}}=\frac{−{n}−\mathrm{1}}{\mathrm{2}} \\ $$

Commented by jagoll last updated on 12/Jan/20

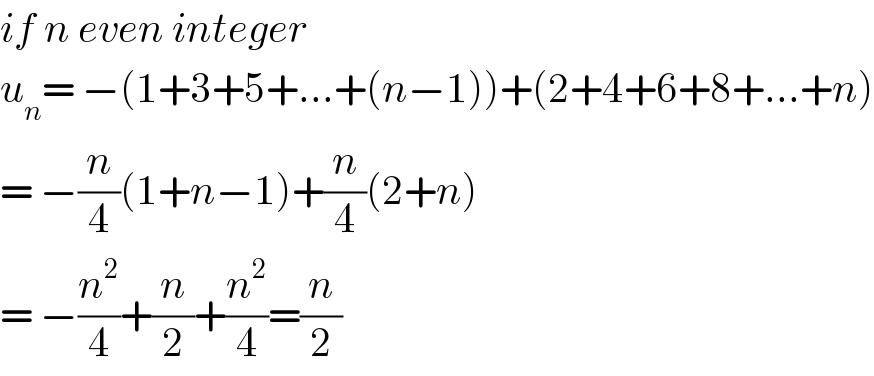
if n even integer u_n = −(1+3+5+...+(n−1))+(2+4+6+8+...+n) = −(n/4)(1+n−1)+(n/4)(2+n) = −(n^2 /4)+(n/2)+(n^2 /4)=(n/2)

$${if}\:{n}\:{even}\:{integer} \\ $$$${u}_{{n}} =\:−\left(\mathrm{1}+\mathrm{3}+\mathrm{5}+...+\left({n}−\mathrm{1}\right)\right)+\left(\mathrm{2}+\mathrm{4}+\mathrm{6}+\mathrm{8}+...+{n}\right) \\ $$$$=\:−\frac{{n}}{\mathrm{4}}\left(\mathrm{1}+{n}−\mathrm{1}\right)+\frac{{n}}{\mathrm{4}}\left(\mathrm{2}+{n}\right) \\ $$$$=\:−\frac{{n}^{\mathrm{2}} }{\mathrm{4}}+\frac{{n}}{\mathrm{2}}+\frac{{n}^{\mathrm{2}} }{\mathrm{4}}=\frac{{n}}{\mathrm{2}} \\ $$

Commented by mr W last updated on 12/Jan/20

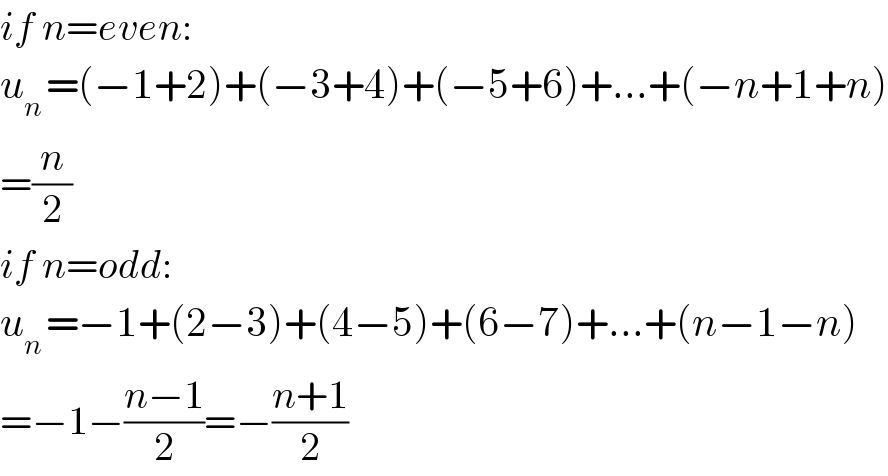
if n=even: u_(n ) =(−1+2)+(−3+4)+(−5+6)+...+(−n+1+n) =(n/2) if n=odd: u_(n ) =−1+(2−3)+(4−5)+(6−7)+...+(n−1−n) =−1−((n−1)/2)=−((n+1)/2)

$${if}\:{n}={even}: \\ $$$${u}_{{n}\:} =\left(−\mathrm{1}+\mathrm{2}\right)+\left(−\mathrm{3}+\mathrm{4}\right)+\left(−\mathrm{5}+\mathrm{6}\right)+...+\left(−{n}+\mathrm{1}+{n}\right) \\ $$$$=\frac{{n}}{\mathrm{2}} \\ $$$${if}\:{n}={odd}: \\ $$$${u}_{{n}\:} =−\mathrm{1}+\left(\mathrm{2}−\mathrm{3}\right)+\left(\mathrm{4}−\mathrm{5}\right)+\left(\mathrm{6}−\mathrm{7}\right)+...+\left({n}−\mathrm{1}−{n}\right) \\ $$$$=−\mathrm{1}−\frac{{n}−\mathrm{1}}{\mathrm{2}}=−\frac{{n}+\mathrm{1}}{\mathrm{2}} \\ $$

Commented by jagoll last updated on 12/Jan/20

waw i′m glad sir. my answer same with you answer

$${waw}\:{i}'{m}\:{glad}\:{sir}.\:{my}\:{answer}\:{same}\:{with}\:{you}\:{answer} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com