Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 115449 by mathmax by abdo last updated on 25/Sep/20

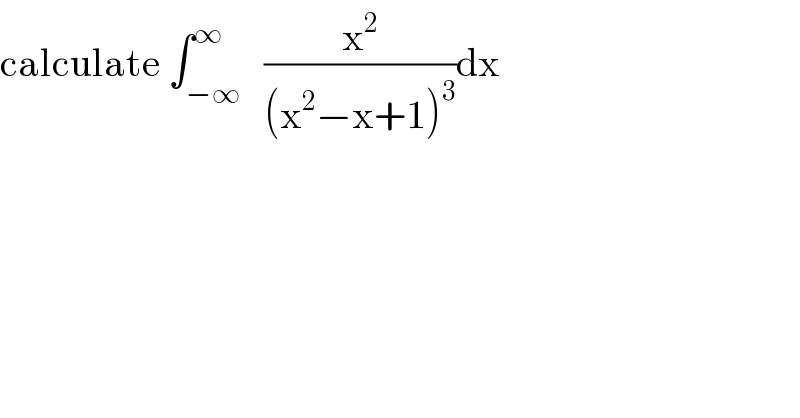
calculate ∫_(−∞) ^∞ (x^2 /((x^2 −x+1)^3 ))dx

$$\mathrm{calculate}\:\int_{−\infty} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dx} \\ $$

Answered by MJS_new last updated on 25/Sep/20

∫(x^2 /((x^2 −x+1)^3 ))dx= [Ostrogeadski] =((2x^3 −3x^2 +2x−2)/(6(x^2 −x+1)^2 ))+(1/3)∫(dx/(x^2 −x+1))= =((2x^3 −3x^2 +2x−2)/(6(x^2 −x+1)^2 ))+((2(√3))/9)arctan (((√3)(2x−1))/( 3)) +C ⇒ answer is ((2(√3))/9)π

$$\int\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{3}} }{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogeadski}\right] \\ $$$$=\frac{\mathrm{2}{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{2}}{\mathrm{6}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}= \\ $$$$=\frac{\mathrm{2}{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{2}}{\mathrm{6}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\:\mathrm{3}}\:+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\pi \\ $$

Commented by mathmax by abdo last updated on 26/Sep/20

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mathmax by abdo last updated on 26/Sep/20

A =∫_(−∞) ^(+∞) (x^2 /((x^2 −x+1)^3 ))dx we have x^2 −x+1 =x^2 −2(x/2) +(1/4) +(3/4) =(x−(1/2))^2 +(3/4) we do the changement x−(1/2) =((√3)/2)t ⇒ A =∫_(−∞) ^(+∞) ((((1/2)+((√3)/2)t)^2 )/(((3/4)(1+t^2 ))^3 )).((√3)/2)dt =((√3)/8).(4^3 /3^3 ) ∫_(−∞) ^(+∞) ((((√3)t+1)^2 )/((t^2 +1)^3 ))dt =((8(√3))/(27)) ∫_(−∞) ^(+∞) ((3t^2 +2(√3)t +1)/((t^2 +1)^3 ))dt =((8(√3))/(27))∫_(−∞) ^(+∞) ((3t^2 +1)/((t^2 +1)^3 ))dt +((8(√3))/(27))∫_(−∞) ^(+∞) ((2(√3)t)/((t^2 +1)^3 ))dt(→=0) =((8(√3))/(27)) ∫_(−∞) ^(+∞) ((3t^2 +1)/((t^2 +1)^3 ))dt let ϕ(z) =((3z^2 +1)/((z^2 +1)^3 )) ⇒ϕ(z) =((3z^2 +1)/((z−i)^3 (z+i)^3 )) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,i) and Res(ϕ,i) =lim_(z→i) (1/((3−1)!)){(z−i)^3 ϕ(z)}^((2)) =(1/2)lim_(z→i) {((3z^2 +1)/((z+i)^3 ))}^((2)) =(1/2)lim_(z→i) {((6z(z+i)^3 −3(z+i)^2 (3z^2 +1))/((z+i)^6 ))}^((1)) =(1/2)lim_(z→i) {((6z(z+i)−3(3z^2 +1))/((z+i)^4 ))}^((1)) =(1/2)lim_(z→i) {((−3z^2 +6iz−3)/((z+i)^4 ))}^((1)) =(1/2)lim_(z→i) (((−6z+6i)(z+i)^4 −4(z+i)^3 (−3z^2 +6iz −3))/((z+i)^8 )) =(1/2)lim_(z→i) (((−6z+6i)(z+i)−4(−3z^2 +6iz −3))/((z+i)^5 )) =(1/2).((−4(3−9))/((2i)^5 )) =((24)/(2.2^5 .i)) =((12)/(2^5 i)) =((2^2 .3)/(2^5 i)) =(3/(8i)) ⇒∫_(−∞) ^(+∞) ϕ(z)dz =2iπ.(3/(8i)) =((3π)/4) ⇒A =((8(√3))/(27)).((3π)/4) =((2π(√3))/9)

$$\mathrm{A}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\:=\mathrm{x}^{\mathrm{2}} −\mathrm{2}\frac{\mathrm{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$=\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{A}\:=\int_{−\infty} ^{+\infty} \:\:\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{t}\right)^{\mathrm{2}} }{\left(\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\right)^{\mathrm{3}} }.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{dt}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{8}}.\frac{\mathrm{4}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{3}} }\:\int_{−\infty} ^{+\infty} \:\frac{\left(\sqrt{\mathrm{3}}\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{27}}\:\int_{−\infty} ^{+\infty} \frac{\mathrm{3t}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}\mathrm{t}\:+\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dt}\:\:=\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{27}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{3t}^{\mathrm{2}} \:+\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dt}\:+\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{27}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{2}\sqrt{\mathrm{3}}\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dt}\left(\rightarrow=\mathrm{0}\right) \\ $$$$=\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{27}}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{3t}^{\mathrm{2}} \:+\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dt}\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{3z}^{\mathrm{2}} \:+\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{3z}^{\mathrm{2}} \:+\mathrm{1}}{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{3}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} } \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:\mathrm{and}\: \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{3}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{3}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\left\{\frac{\mathrm{3z}^{\mathrm{2}} +\mathrm{1}}{\left({z}+{i}\right)^{\mathrm{3}} }\right\}^{\left(\mathrm{2}\right)} \:=\frac{\mathrm{1}}{\mathrm{2}}{lim}_{{z}\rightarrow\mathrm{i}} \:\:\left\{\frac{\mathrm{6z}\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{3z}^{\mathrm{2}} +\mathrm{1}\right)}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{6}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\left\{\frac{\mathrm{6z}\left(\mathrm{z}+\mathrm{i}\right)−\mathrm{3}\left(\mathrm{3z}^{\mathrm{2}} +\mathrm{1}\right)}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\left\{\frac{−\mathrm{3z}^{\mathrm{2}} +\mathrm{6iz}−\mathrm{3}}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\frac{\left(−\mathrm{6z}+\mathrm{6i}\right)\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} −\mathrm{4}\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} \left(−\mathrm{3z}^{\mathrm{2}} +\mathrm{6iz}\:−\mathrm{3}\right)}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{8}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\frac{\left(−\mathrm{6z}+\mathrm{6i}\right)\left(\mathrm{z}+\mathrm{i}\right)−\mathrm{4}\left(−\mathrm{3z}^{\mathrm{2}} +\mathrm{6iz}\:−\mathrm{3}\right)}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{5}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\frac{−\mathrm{4}\left(\mathrm{3}−\mathrm{9}\right)}{\left(\mathrm{2i}\right)^{\mathrm{5}} }\:=\frac{\mathrm{24}}{\mathrm{2}.\mathrm{2}^{\mathrm{5}} .\mathrm{i}}\:=\frac{\mathrm{12}}{\mathrm{2}^{\mathrm{5}} \mathrm{i}}\:=\frac{\mathrm{2}^{\mathrm{2}} .\mathrm{3}}{\mathrm{2}^{\mathrm{5}} \mathrm{i}}\:=\frac{\mathrm{3}}{\mathrm{8i}}\:\Rightarrow\int_{−\infty} ^{+\infty} \varphi\left(\mathrm{z}\right)\mathrm{dz} \\ $$$$=\mathrm{2i}\pi.\frac{\mathrm{3}}{\mathrm{8i}}\:=\frac{\mathrm{3}\pi}{\mathrm{4}}\:\Rightarrow\mathrm{A}\:=\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{27}}.\frac{\mathrm{3}\pi}{\mathrm{4}}\:=\frac{\mathrm{2}\pi\sqrt{\mathrm{3}}}{\mathrm{9}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com