Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 62669 by Sayantan chakraborty last updated on 24/Jun/19

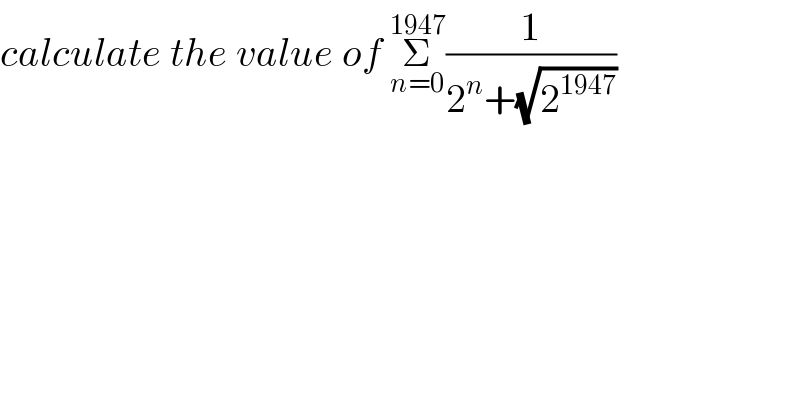
calculate the value of Σ_(n=0) ^(1947) (1/(2^n +(√2^(1947) )))

$${calculate}\:{the}\:{value}\:{of}\:\underset{{n}=\mathrm{0}} {\overset{\mathrm{1947}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} +\sqrt{\mathrm{2}^{\mathrm{1947}} }} \\ $$

Answered by tanmay last updated on 24/Jun/19

a=(√2^(1947) ) S=(1/(2^0 +a))+(1/(2^1 +a))+(1/(2^2 +a))+(1/(2^3 +a))+...+(1/(2^(1947) +a)) ((2+a)/2)≥(2×a)^(1/2) 2+a≥2×(2a)^(1/2) (1/(2+a))≤(1/(2×(2a)^(1/2) )) (1/(2+a))≤(1/(2(√a) ×(2)^(1/2) )) S≤(1/(2(√a)))[(1/((2^0 )^(1/2) ))+(1/((2^1 )^(1/2) ))+(1/((2^2 )^(1/2) ))+...+(1/((2^(1947) )^(1/2) ))] S≤(1/(2(√a)))[(1/(((√(2 )) )^0 ))+(1/(((√2) )^1 ))+(1/(((√2) )^2 ))+...+(1/(((√2) )^(1947) ))] S≤(1/(2(√a)))×(((1/(((√2) )^0 )){1−((1/((√2) )))^(1948) })/(1−((1/(√2))))) [using ((A(1−r^n ))/(1−r))] S≤(1/(2(√a)))×(((√2)×(1−(1/2^(974) )))/((√2) −1)) S≤(1/((2−(√2) ))) ×((1−(1/2^(974) ))/(((√2^(1947) ) )^(1/2) ))≈(1/((2−(√2) )))×(1/(((√2^(1947) ) )^(1/2) )) i have found approximate value not exact value so please cheack

$${a}=\sqrt{\mathrm{2}^{\mathrm{1947}} }\: \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} +{a}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} +{a}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} +{a}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} +{a}}+...+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1947}} +{a}} \\ $$$$\frac{\mathrm{2}+{a}}{\mathrm{2}}\geqslant\left(\mathrm{2}×{a}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{2}+{a}\geqslant\mathrm{2}×\left(\mathrm{2}{a}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}+{a}}\leqslant\frac{\mathrm{1}}{\mathrm{2}×\left(\mathrm{2}{a}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}+{a}}\leqslant\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}\:×\left(\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$${S}\leqslant\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}}\left[\frac{\mathrm{1}}{\left(\mathrm{2}^{\mathrm{0}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }+\frac{\mathrm{1}}{\left(\mathrm{2}^{\mathrm{1}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }+\frac{\mathrm{1}}{\left(\mathrm{2}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }+...+\frac{\mathrm{1}}{\left(\mathrm{2}^{\mathrm{1947}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }\right] \\ $$$${S}\leqslant\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}}\left[\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}\:}\:\right)^{\mathrm{0}} }+\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}\:\right)^{\mathrm{1}} }+\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} }+...+\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}\:\right)^{\mathrm{1947}} }\right] \\ $$$${S}\leqslant\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}}×\frac{\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}\:\right)^{\mathrm{0}} }\left\{\mathrm{1}−\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}\:}\right)^{\mathrm{1948}} \right\}}{\mathrm{1}−\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)}\:\left[{using}\:\frac{{A}\left(\mathrm{1}−{r}^{{n}} \right)}{\mathrm{1}−{r}}\right] \\ $$$${S}\leqslant\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}}×\frac{\sqrt{\mathrm{2}}×\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{974}} }\right)}{\sqrt{\mathrm{2}}\:−\mathrm{1}} \\ $$$${S}\leqslant\frac{\mathrm{1}}{\left(\mathrm{2}−\sqrt{\mathrm{2}}\:\right)}\:×\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{974}} }}{\left(\sqrt{\mathrm{2}^{\mathrm{1947}} }\:\:\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }\approx\frac{\mathrm{1}}{\left(\mathrm{2}−\sqrt{\mathrm{2}}\:\right)}×\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}^{\mathrm{1947}} }\:\right)^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$\boldsymbol{{i}}\:\boldsymbol{{have}}\:\boldsymbol{{found}}\:\boldsymbol{{approximate}}\:\boldsymbol{{value}}\:\boldsymbol{{not}} \\ $$$$\boldsymbol{{exact}}\:\boldsymbol{{value}}\:\boldsymbol{{so}}\:\boldsymbol{{please}}\:\boldsymbol{{cheack}} \\ $$

Commented by Sayantan chakraborty last updated on 25/Jun/19

answer is ((487)/((√)2^(1945) )).

$${answer}\:{is}\:\frac{\mathrm{487}}{\sqrt{}\mathrm{2}^{\mathrm{1945}} }. \\ $$

Answered by ajfour last updated on 30/Jun/19

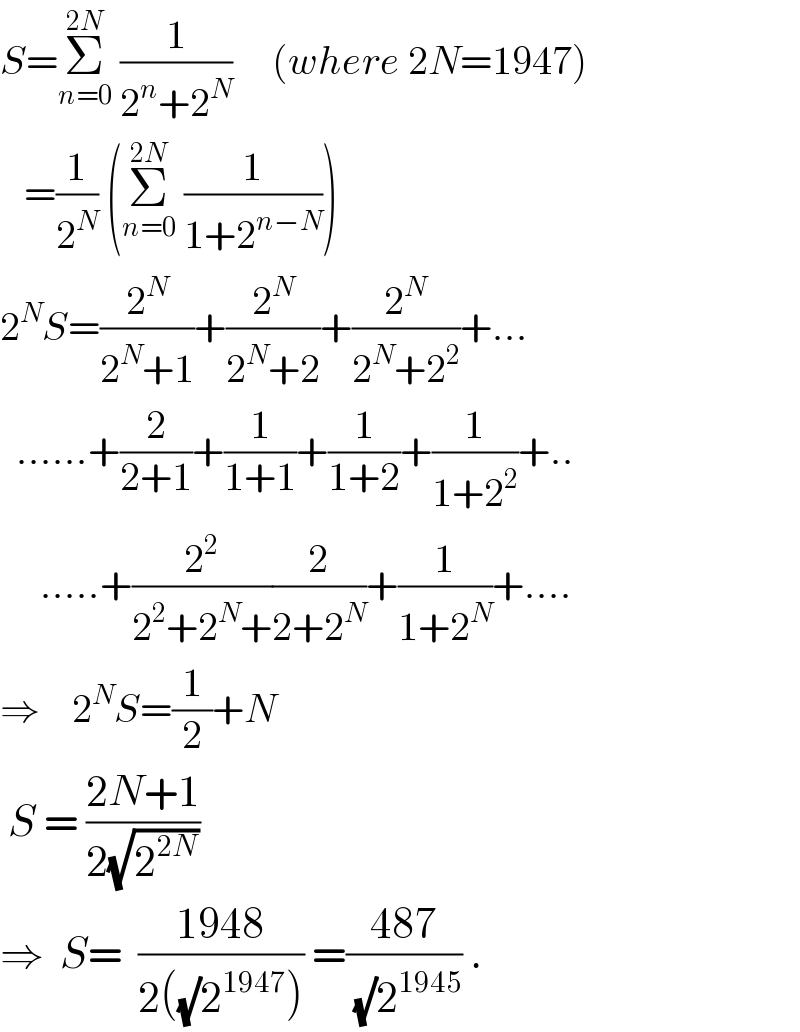
S=Σ_(n=0) ^(2N) (1/(2^n +2^N )) (where 2N=1947) =(1/2^N ) (Σ_(n=0) ^(2N) (1/(1+2^(n−N) ))) 2^N S=(2^N /(2^N +1))+(2^N /(2^N +2))+(2^N /(2^N +2^2 ))+... ......+(2/(2+1))+(1/(1+1))+(1/(1+2))+(1/(1+2^2 ))+.. .....+(2^2 /(2^2 +2^N +))(2/(2+2^N ))+(1/(1+2^N ))+.... ⇒ 2^N S=(1/2)+N S = ((2N+1)/(2(√2^(2N) ))) ⇒ S= ((1948)/(2((√)2^(1947) ))) =((487)/((√)2^(1945) )) .

$${S}=\underset{{n}=\mathrm{0}} {\overset{\mathrm{2}{N}} {\sum}}\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} +\mathrm{2}^{{N}} }\:\:\:\:\:\left({where}\:\mathrm{2}{N}=\mathrm{1947}\right) \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}^{{N}} }\:\left(\underset{{n}=\mathrm{0}} {\overset{\mathrm{2}{N}} {\sum}}\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{{n}−{N}} }\right) \\ $$$$\mathrm{2}^{{N}} {S}=\frac{\mathrm{2}^{{N}} }{\mathrm{2}^{{N}} +\mathrm{1}}+\frac{\mathrm{2}^{{N}} }{\mathrm{2}^{{N}} +\mathrm{2}}+\frac{\mathrm{2}^{{N}} }{\mathrm{2}^{{N}} +\mathrm{2}^{\mathrm{2}} }+... \\ $$$$\:\:......+\frac{\mathrm{2}}{\mathrm{2}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\mathrm{2}} }+.. \\ $$$$\:\:\:\:\:.....+\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{{N}} +}\frac{\mathrm{2}}{\mathrm{2}+\mathrm{2}^{{N}} }+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{{N}} }+.... \\ $$$$\Rightarrow\:\:\:\:\mathrm{2}^{{N}} {S}=\frac{\mathrm{1}}{\mathrm{2}}+{N} \\ $$$$\:{S}\:=\:\frac{\mathrm{2}{N}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}^{\mathrm{2}{N}} }}\:\: \\ $$$$\Rightarrow\:\:{S}=\:\:\frac{\mathrm{1948}}{\mathrm{2}\left(\sqrt{}\mathrm{2}^{\mathrm{1947}} \right)}\:=\frac{\mathrm{487}}{\sqrt{}\mathrm{2}^{\mathrm{1945}} }\:. \\ $$

Commented by Sayantan chakraborty last updated on 30/Jun/19

Yes it is correct solution.

$$\boldsymbol{{Yes}}\:\boldsymbol{{it}}\:\boldsymbol{{is}}\:\boldsymbol{{correct}}\:\boldsymbol{{solution}}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com