
Question Number 160928 by mnjuly1970 last updated on 09/Dec/21
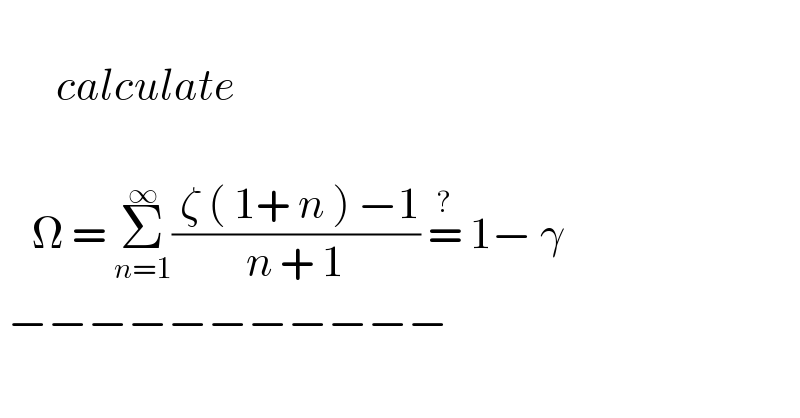
$$ \\ $$$$\:\:\:\:\:\:\:{calculate} \\ $$$$ \\ $$$$\:\:\:\:\Omega\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\zeta\:\left(\:\mathrm{1}+\:{n}\:\right)\:−\mathrm{1}}{{n}\:+\:\mathrm{1}}\:\overset{?} {=}\:\mathrm{1}−\:\gamma\: \\ $$$$\:−−−−−−−−−−− \\ $$
Answered by qaz last updated on 09/Dec/21
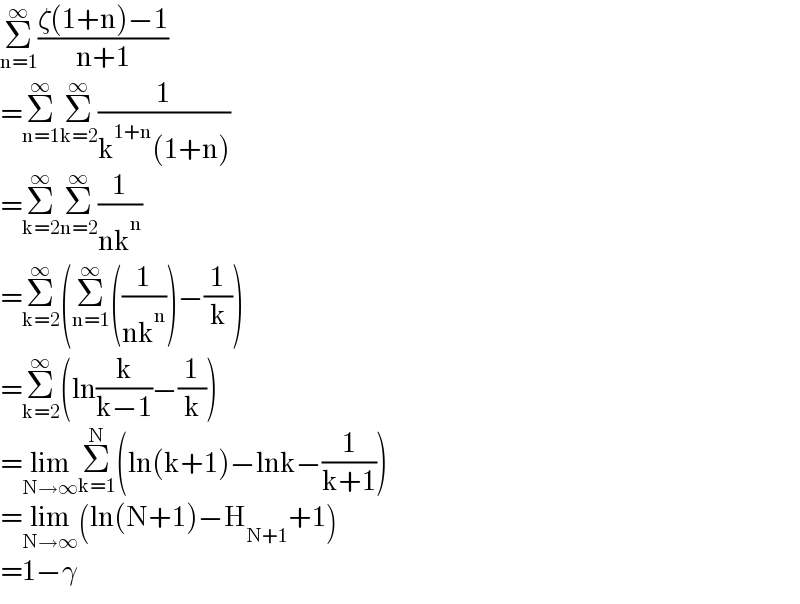
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\zeta\left(\mathrm{1}+\mathrm{n}\right)−\mathrm{1}}{\mathrm{n}+\mathrm{1}} \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\mathrm{k}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{1}+\mathrm{n}} \left(\mathrm{1}+\mathrm{n}\right)} \\ $$$$=\underset{\mathrm{k}=\mathrm{2}} {\overset{\infty} {\sum}}\underset{\mathrm{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{nk}^{\mathrm{n}} } \\ $$$$=\underset{\mathrm{k}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{nk}^{\mathrm{n}} }\right)−\frac{\mathrm{1}}{\mathrm{k}}\right) \\ $$$$=\underset{\mathrm{k}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\mathrm{ln}\frac{\mathrm{k}}{\mathrm{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{k}}\right) \\ $$$$=\underset{\mathrm{N}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\left(\mathrm{ln}\left(\mathrm{k}+\mathrm{1}\right)−\mathrm{lnk}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\right) \\ $$$$=\underset{\mathrm{N}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{ln}\left(\mathrm{N}+\mathrm{1}\right)−\mathrm{H}_{\mathrm{N}+\mathrm{1}} +\mathrm{1}\right) \\ $$$$=\mathrm{1}−\gamma \\ $$
Commented by mnjuly1970 last updated on 09/Dec/21

$${bravo}\:{sir}\:{qaz} \\ $$
