
Question Number 188449 by mnjuly1970 last updated on 01/Mar/23
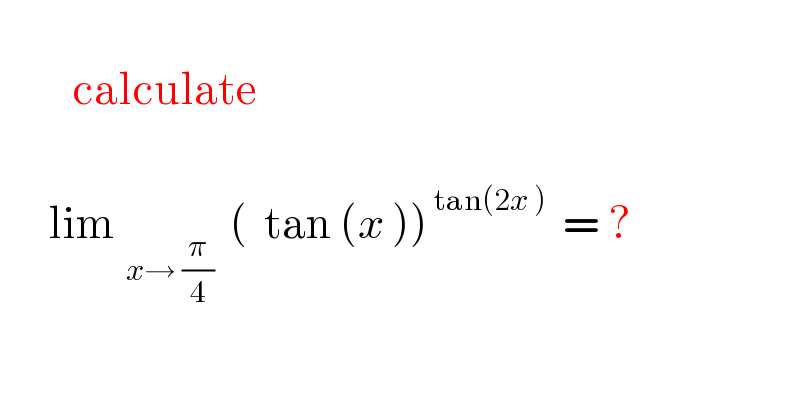
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{calculate} \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\mathrm{lim}_{\:\:{x}\rightarrow\:\frac{\pi}{\mathrm{4}}} \:\:\left(\:\:\mathrm{tan}\:\left({x}\:\right)\right)^{\:\mathrm{tan}\left(\mathrm{2}{x}\:\right)} \:\:=\:?\:\:\: \\ $$$$\:\: \\ $$
Answered by cortano12 last updated on 01/Mar/23
![L=lim_(x→(π/4)) [tan x ]^(tan 2x) L = e^(lim_(x→(π/4)) (((tan x−1)/(tan 2x)))) L = e^(lim_(x→(π/4)) ((sin x−cos x)/(cos x)). ((sin 2x)/((cos x−sin x)(cos x+sin x)))) L = e^(lim_(x→(π/4)) [((−sin 2x)/(cos x(cos x+sin x))) ]) L = e^(−((1/((1/( (√2)))((√2) ))))) = (1/e)](Q188450.png)
$$\:\mathrm{L}=\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\left[\mathrm{tan}\:\mathrm{x}\:\right]^{\mathrm{tan}\:\mathrm{2x}} \\ $$$$\:\mathrm{L}\:=\:\mathrm{e}^{\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\left(\frac{\mathrm{tan}\:\mathrm{x}−\mathrm{1}}{\mathrm{tan}\:\mathrm{2x}}\right)} \\ $$$$\:\mathrm{L}\:=\:\mathrm{e}^{\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}}.\:\frac{\mathrm{sin}\:\mathrm{2x}}{\left(\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right)\left(\mathrm{cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}\right)}} \\ $$$$\:\mathrm{L}\:=\:\mathrm{e}^{\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\left[\frac{−\mathrm{sin}\:\mathrm{2x}}{\mathrm{cos}\:\mathrm{x}\left(\mathrm{cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}\right)}\:\right]} \\ $$$$\:\mathrm{L}\:=\:\mathrm{e}^{−\left(\frac{\mathrm{1}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\sqrt{\mathrm{2}}\:\right)}\right)} \:=\:\frac{\mathrm{1}}{\mathrm{e}} \\ $$
Commented by mnjuly1970 last updated on 03/Mar/23

$${thx}\:{alot}\:{sir}\:{cortano} \\ $$
